福島県教育センター所報ふくしま　No.72（S60/1985.8） -005/038page

中学校教材

ロータリーエンジンの作動模型製作

科学技術教育部　 斎藤　一哉

1．　はじめに

　機械2学習における発展教材として，又は選択技術科における教材として活用できるロータリーエンジンをとり上げてみた。
　NSU−Wankelエンジンの登場を契機に，一躍注目を集めたロータリーエンジンもその歴史は古く，アイディアの発端は16世紀にさかのぼるといわれている。出力の割にコンパクトで，振動，騒音が少ない，また構造が簡単で部品数が少いなどレシプロエンジンと比べ数々の利点をもちながら内燃機関としての実用化の歴史はまだ浅く，今後更に改良されていくものと思われる。
　このエンジンのハウジング及びロータの作図や模型工作を通して，ロータリーエンジンの回転原理と作動を理解させることができる。

2．　ロータリーエンジン模型の設計

　現在実用化されているロータリーエンジンは，公転ピストン構造を基本とするNSU−Wankelエンジンであり，そのロータハウジングとロータの作図を通し，ロータリーエンジンの回転原理をつかませる。

（1）ロータハウジングの輪郭　−　エピ・トロコイド曲線の作図
　ロータハウジングの輪郭にはエビ・トロコイド曲線が用いられている。これは図1に示すように固定された基円Aの外周を転がり円Bが内接して転がるとき，転がり円の直径上の円周外の定点Pが描く曲線である。
　この曲線を求める数式については所報第71号の＜目で見る資料＞に，当教育センターの電子計算機システムとN・Cフライス盤によるロータリーエンジン模型の製作として掲載してあるので参考にしていただきたいが，学校現場でこの曲線を描かせるには別の方法を考える必要がある。
　図1（a）の位置から転がり円Bが基円A上をθだけ回転し，図（b）の状態になったとき，転がり円B自身の回転角φは，二つの円A，Bの回転比から
　　　　　　φ ＝ R／r・θ
　また，図1（b）で，転がり円Bの中心からX軸に平行なX'軸を引くと，定点PのX軸に対する回転角ψは，図から判るように
　　　　　　ψ ＝ θ−φ ＝ (1−R／r)θ
　作図データとして　R＝20mm　r＝30mm　L＝69mとすると
　　　　　　e ＝ r−R ＝ 10，　R／r ＝ 2／3
　となって，転がり円が基円上をθだけ転がったとき，P点はX軸に対して(1−R／r)θ ＝ θ／3だけ回転することになる。これをθ ＝ 0°〜360°についてP点の位置を作図していけば，正しいエビ・トロコイド曲線を描いていくことができる。
　このエビ・トロコイド曲線を描くために教具化


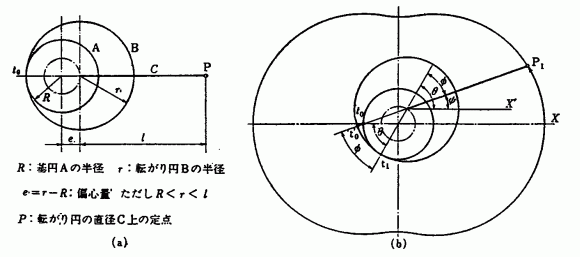
　　　　　　　　図1　エビ・トロコイド曲線の作図