福島県教育センター所報ふくしま　No.74（S60/1985.12） -004/038page

1，2，3cmなどとするとかきやすい。

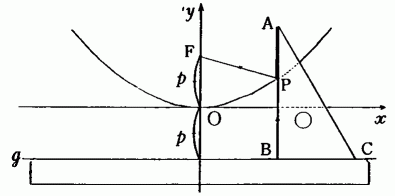
　　　　　　　　図　2

（2）円を利用する方法
　放物線 y ² ＝ 8x をかくには，点F（2，0）を中心とする半径（k＋2）cmの円と，直線 x ＝ k （k＝0.5，1，2，3，……，8）との交点を図 3のように結ぶ。
　曲線をノートにかくときは，座標軸の1目盛りの長さを1cmとするとかきやすい。

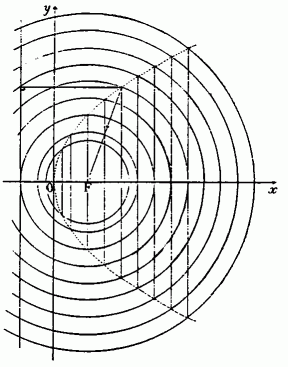
　　　　　　　　図　3

（3）長方形を利用する方法
　AB ＝ b，BC ＝ a なる長方形ABCDを図 4のようにとる。辺AB，BCをそれぞれn等分して i＝1，2，3，………，n−1の各場合についてP _i からBCに平行線を引き線分AQ _i との交点をR _i とすれば，点A，R ₁ ，R ₂ ，……，R _n−1 ，CはAを頂点，ADを軸とする放物線
　　　y ² ＝（b ² /a)x
上にある。これは，H（x，0），K（ia/n，0）R _i （x，y）とすると△AR _i Hと△AQ _i Kとが相似であることから導かれる。

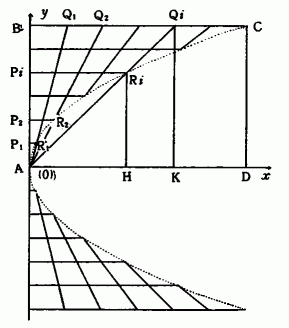
　　　　　　　　図　4
　放物線 y ² ＝ 4x をかくときは，（a，b）＝ （4，4），（9，6），（16，8）などとすると等分しやすい。図 5は（16，8）の場合である。

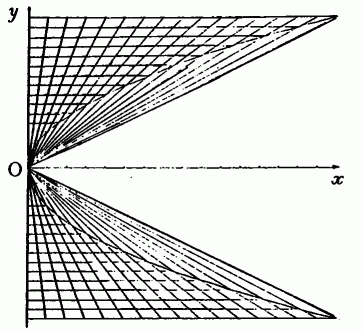
　　　　　　　　図　5

5．おわりに

　以上，放物線の導入の工夫と曲線のかきかたについて述べてみたが，二次曲線では数式の計算が煩雑になりがちであるので，できるだけ図形と関連させて指導することが大切と思われる。

参考図書
• 文部省　高等学校学習指導要領解説　数学編
• 田島一郎，福森信夫編集　改訂　高等学校学習指導要領の展開（明治図書）
• 穂刈四三二　市民の数学（共立出版）
• 昭和58年度用教科書　高等学校　代数・幾何（13社）