福島県教育センター所報ふくしま　No.74（S60/1985.12） -003/038page

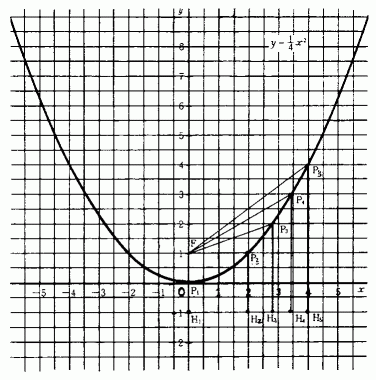
P i F ＝ P i H i なる点 H i （P i H i は x軸に垂直）が直線 y ＝ -1 上に並んでいることを確かめる。 （展開）		グラフの対称性を利用して第1象限で考えさせる。 （図 1）
3. 曲線上の任意の点 P から，PF ＝ PH なる点H（PHは x軸に垂直）をとる。Hが直線 y ＝ -1 上にあることを確かめる。	10分	測定による。 予想される生徒の関心 「点Fをどのようにして（0，1）に決めたのか」 2点間の距離の公式を確認させる。
5. 4.によって，放物線 y ＝(1/4)x 2 は，どんな点の焦合であるかを考える。		放物線の定義に気づかせる。
6. 資料 2の曲線について，F（0，1/2），直線を y = -1/2 として 3.，4.，5.に準じて確かめ，考える。	5分	曲線を変えても，性質の変わらないことに気づかせる。 （資料 2）
7. 放物線の定義を確認する。		放物線の定義をする。
8. P（x，y）　F（0，p）　H（x，-p）として， 定義 PF ＝ PH より x 2 ＝ 4py を導く。	10分	式の変形における同値関係を確認させる。
9. 資料 1，2の曲線について，8.の p の値を求める。		pの値の図形上の意味を理解させる。
10. 図 1の曲線を横にしても，PF ＝ PH の性質は保存されることから P（x，y） F（p，0） H（-p，y）として， 定義 PF ＝ PH より y 2 ＝4pxを導く。	15分	だ円，双曲線との統一をはかるために，準線を x軸 に垂直に，焦点を x軸上にとる。二次関数のグラフとの関連を強調する場合は，準線を x軸に平行にとるようにさせる。 方程式が簡潔に表されることを理解させる。
11. 放物線の焦点，準線，頂点，軸について，その幾何学的な意味を理解する。
12. 8.，10.のようにP，F，Hの座標をとる理由を考える。 （終末）
13. 本時のまとめをする。	5分
14. 次時の予告を聞く。

　　　　　　　　図　1

4．放物線のかきかた

（1）定規を利用する方法
　放物線 x2 ＝ 4py をかくには，図 2のように原点Oから定直線g及び定点Fまでの距離をそれぞれpとする。三角定規ABCの辺ABに等しい長さの糸の両端をAとFに固定する。糸を鉛筆の先Pで張りながら三角定規をgに沿って移動すれば，PF ＝ PB よりPはFを焦点，gを準線とする放物線 x2＝4py をえがく。
　曲線をノートにかくときは，座標軸の1目盛りの長さを1cm，糸の長さを8cm〜20cm，p＝