福島県教育センター所報ふくしま　No.78（S61/1986.10） -030/038page

あろう。つまり，○この教材で何を教えるかという教師の願いを，情動・論理の両面から追究する。さらに，○この願いを教師のはたらきかけとして具体化するということである。

（2）授業の設計

教材研究

　 1　専門的な立場での教材研究
　＜歴史的な発生について＞
　　○「三平方の定理」に関しては，ピタゴラスが若い頃エジプトに留学したとき，寺院の石畳みの形からヒントをえて考えついた等
　　○この定理の証明は，歴史の古い有名なものだけに，多くの方法が考えられていること
　　○この定理のわが国への伝来についてなど，書物を通して数多くの知識を得ることができる。
　＜歴史的な展開と現況について＞
　数学研究の最先端で，「三平方の定理」がどのように考えられているのか。このことについての理解は十分にもち合わせてはいないが，専門的な数学書から学ぶ姿勢があれば，いくらでも知識や理解を深めていくことができるはずである。
　○ユークリッド「原論」でも主題の1つで，そこでは，面積の定理として扱われている。
　○平面上だけではなく，空間では直方体の対角線の長さ 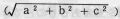ということに広がり．さらにｎ次元，無限次元へと拡張されて，現代数学の根幹になっている。
　○定理の拡張について（例）


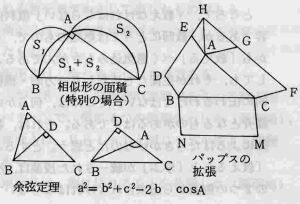
　専門的な数学研究は，自分の数学的な知識の背景，本質的な理解，さらに数学を応用した世界についての知識の豊かさを形づくることになる。
＜教育の歴史と現況について＞
　「三平方の定理」が，数学教育の歴史の流れの中でどのように考えられ，取り扱われてきたのか。このことは，授業をしくむ上で十分に考察を加えなければならない事柄と考える。学習指導要領，指導者，教科書，その他の教育図書や実践記録などでの研究を欠かせない。
　○学習指導要領では，「図形の計量」に関する目標と内容が示されている。
　○「ピタゴラスの定理」から「三平方の定理」への名称の変更にかかわること。
　○定理にまつわるエピソードやピタゴラスに関する話にふれて，学習に対する興味・関心，数学史的な興味を喚起する好材料であること。
　○取り扱いの上では，特に発見的な考えの指導に十分役立てられる。ただ，「3・4・5の原理」と「三平方の定理」との間には大きな開きのある点に注意を向けたい。（特殊から一般へ）
　○定理の証明のとりあげ方と論証指導について
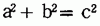　○ で，2つを知って残りを求めるという具体的な応用と平方根の概念・平方根表の使用法，2次方程式などとの関連づけ
　○使用する場が多いので，知識としての習得と図形の計量への活用という両面からの指導を心がける。
　○この定理は，「数学的な考え方」を育てることにねらいをおいた指導ができる。
などである。

　 2　生徒の世界からみる教材研究
　

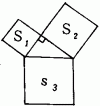
　2年生で「等積変形」の学習後応用的にＳ 1 ＋Ｓ 2 ＝Ｓ 3 を扱っている。その際，軽く「三平方の定理」にふれてはいるが，この定理を知っているという生徒は3〜4名，しかし，性質・内容を正確に言えるものはいなかった。この学習を進めていく中で，生徒たちはどのような困難を見い出しながら，ど