福島県教育センター所報ふくしま　No.78（S61/1986.10） -031/038page

う理解していくのか。生徒の目を通して教材をみるというのは，生徒たちの「わかりかた」をわかるためにも是非必要なことである。他者を理解する教師として，人間としての柔軟さと奥ゆきの深さを求められるところである。

3　教える立場からの教材研究
　1，2の教材研究をへて，授業を計画し実践しようとするときに，自分自身としての考え，アイディア，工夫という点で自信がもてず，他人の教材や教材解釈の借り物で授業を終えていることが多い。教師としての「教えたい」ものを明確に把握していないのでは，生徒の「学びたいもの」への転化など望むべくもないであろう。
　この立場からの教材研究（略）にもとづいた＜単元設定の理由＞は，次のようなものになった。

（1）「三平方の定理」は，図形の計量，平面図形や空間図形の性質を考察する上で応用性も高く，重要な定理のひとつである。また，この定理の学習を通して，定理そのものの理解だけでなく，生徒の図形に対する直観力，洞察力を養い，実際の場での問題解決力を高めていくことも期待できる。（2）生徒は図形の学習において，第1学年では，主として空間図形についての性質を幾何学的な操作や計量関係を用いて理解を深め，第2学年では．数学的推論に関する能力を伸ばし，見通しをもって論理的に考察する経験をしてきている。しかし，これ ＿＿＿（以下　略）＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

授業の設定

　以上のような手順をふんだ教材研究をベースに今，生徒たちに「教える」にはどこを問題にして何をどう「教える」のかを考えてみた。これはまた，ひとりひとりの生徒の世界に，今何が必要とされているのか，その必要を満たすために，いつどこで，私は何をなすべきなのかを，教材とのかかわりで具体的に見定めをすることにもなる。
　く単元の目標＞と＜単元の展開計画＞を以下に示してみる。

　＜単元の目標＞

（1）「三平方の定理」とその逆を理解させ，これを平面図形や空間図形の性質の考察や計量などに用いることができるようにする。 （2）図形に対する直観力や洞察力とともに，図形の性質について論理的に考察する力を身につけさせる。

　＜単元の展開計画＞　　単元名　「三平方の定理」　（9時間）
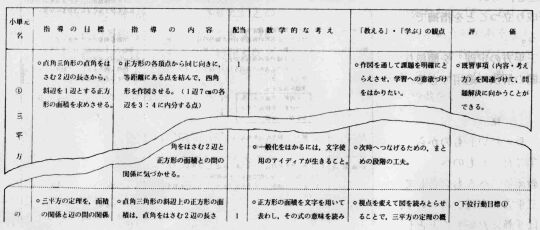