福島県教育センター所報ふくしま　No.82（S62/1987.8） -017/038page

(2)　ジュールの法則　電流の発熱現象をとらえる場合、定量的な実験をするときは熱量計を用いて行ってきた。だが、熱量計を用いた実験では、Q=0.24IEtの公式を導くことはかなりむずかしく、定性的にとらえざるをえない面があった。
　問題点としては、理振法の定電源ではかなりの脈流成分を含んでいること。また、ヒーターとしてのニクロム線の性能、散逸してしまう熱など、正確な実験を行うためにはいくつかの課題がある。
　しかし、身近にあるものを用いて比較的容易にこれらの課題を克服し実験を実施した。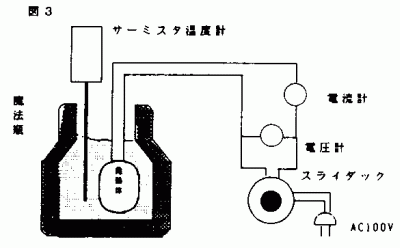

1. 実験方法

　図2に回路図及び全体の写真が示してある。発熱体としてセラミックヒータを用いた。これは水中での安全性が高い。熱量計としては、熱の散逸が少なく保温力の高い魔法瓶を用いた。さらに電源としてスライダックでAC100Vに固定した。　実験では、2.2Lの水を魔法瓶に入れ室温になるまで放置した。(同時に発熱体も入れて置く)1分毎に水温を測定しその結果をグラフ化した。

2.　実験結果について

　電流による仕事をWとすると
　W=Pt(Pは電力、tは秒)――――――――――――1

発熱体から発生する熱量をQとすると
　Q=mcθ(mは質量、cは比熱、θは温度差)―――――2

　発生する熱量は、電流による仕事に比例するから
　W=JQ(Jは熱の仕事当量)――――――――――――3

が成立する。(ジュールの法則)

　表2に側定結果を示してある。この関係を3式に代入してJの値を求めた。その結果はJ=4.0となった。この逆数をとればO.25という値が得られる。
　従って3式は、Q=0.25Ptとなり、一般に教科書で示されているジュールの法則Q=0.24Ptとかなりよい一致を示した。

3．実験上の留意点
　発熱体とサーミスタをできるだけ離し、また魔法瓶中の水が一様に温まるように発熱体を利用してかくはんする必要がある。

4.　効果について　今までは、発熱量は電流・電圧そして時間の積に比例することを理解させるにとどまり、比例定数を正確に求めるまではいたらなかった。　今回の試みでは簡単な装置ではあるが、容易に定数を求めることが可能となり、教科書との関連が図れるようになった。

3.終わりに

　生徒の興味・関心も高めるべく身近な電気製品を用いて実験を行った。今後はマイクロコンピュータを利用した実験なども開発し、生徒にとってわかり易く魅力的な実験なども実施したいと考えている。

＜参考文献＞
「先生と生徒のための物理実験」
(共立出版)