福島県教育センター所報ふくしま　No.96（H02/1990.8） -009/038page

(V)座標軸に平行な直線を軸とする回転原点への平行移動をTa、回転移動をTθ、回転の中心への平行移動をTbとすると


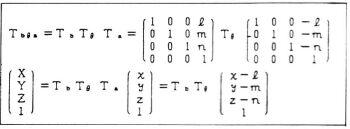
(vi)任意の点を中心とする任意の軸回りの回転
方向余弦を（n、n2、n3）、P=1-cosθとすると

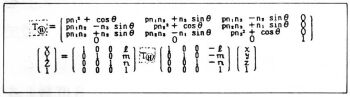
(vii)任意の点を中心とするスケーリング

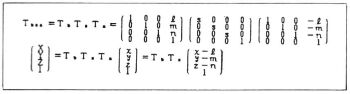
4.透視投影
視点を基準として、3次元図形の座標を変換して遠近をつける処理を透視変換という。また、3次元図形を2次元に投影して2次元図形を表示する処理を投影変換という。両方をあわせて透視投影という。

5.クリッピング
スクリーンの表示範囲よりはみ出した部分を取り去ることをクリッピングという。

まとめと今後の課題
3次元グラフィックス理論の中から、物体の見え方と3次元図形のスクリーンヘの表示ということに焦点をあて、コンピュータによる透視と投影にっいて簡単な直方体をモデルにシミュレーションしてみた。
本研究で用いた理論は、高等学校数学との関わりのある部分を追究しているために、平易な行列の計算式が多く用いられている。また空問に位置する立体図形を動かすための入カデータの形式は、移動方向の入力として方向余弦を用いているため、三角関数の学習としても役立つ部分を持っている。
一般に2次元クリッピングを行う場合には、グラフィックス画面制御命令で簡単にプログラム処理できるが、クリッピングの理論を考察していくと、不等式による領域指定の考え方や、3次元空間における直線の方程式とその交点の問題など、高等学校数学の教材の支援に役立つ領域を多く含んでいる。
本研究で考察した理論と実験は、コンピュータ・グラフィックスの入門の部分であり、今後の研究課題として、奥の深い問題を多く山積している。なかでも陰線処理の理論は、ベクトルの外積や行列式などを用い、難しいといわれている分野でもある。
今日、パーソナル・コンピュータの普及によって、「コンピュータ・グラフィック」』は身近な研究分野として、今後ますます関心が高まっていくに相違ない。
（参考文献）
「入門グラフィックス」佐藤義雄著 アスキー出版局