福島県教育センター所報ふくしま　No.96（H02/1990.8） -008/038page

III 研究の内容

1.はじめに

3次元図形をスクリーン等の平面に表示するためには、実に多くの処理が必要となる。本研究ではワイヤフレームモデルによる、3次元グラフィックスの処理について考えてゆくことにする。
ワイヤフレームモデルをスクリーン上に表示するための手順は次のようになる。
(1)視点座標系(左手系)で3次元図形を定義する。・・・＜形状定義＞
(2)3次元図形の平行移動、回転等の移動後の座標を求める。・・・＜座標変換＞
(3)3次元図形に遠近をつけて、投影面に投影する。・・・＜透視投影＞
(4)3次元図形をスクリーン上の定められた位置に表示する。・・・＜ビューポート変換＞
(5)スクリーンの表示範囲よりはみ出した部分を取り去る・・・＜クリッピング＞

2.形状定義
ワイヤフレームモデルでは、物体の各頂点の座標値と、これらの頂点を結ぶ稜線のつながり具合を、データとして定義する必要がある。それには各頂点に番号をつけ、各頂点の座標値を定義したうえで、つながっている2つの頂点の番号を示すことで、結びつきの状態を定義する。

3.座標変換
座標原点に視点をおいた視点座標系（左手系）を用いると、視点移動に伴う座標変換の処理は、比較的簡単にできる。3次元の移動量を、視点の移動量で表すことにすると、3次元の物体は逆の方向に移動したように見える。
視点が移動して、3次元空間の点P(X、Y、Z)が点P'(X、Y、Z)に移動したものとして、以下の移動や回転を考える。
(1)視点の平行移動
X、Y、Z各軸方向の視点の移動量をそれぞれl、ｍ、ｎとすると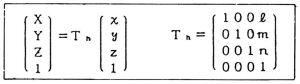

(2)視点(座標軸回り)の回転
視点座標系の座標軸回りの回転は、X軸回りについてはYからZへ、Y軸回りについてはZからXへ、Z軸回りについてはXからYへの回転を正の方向とする。
(i)視点のX軸回りの回転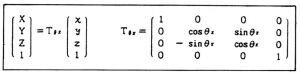

(ii)視点のY軸回りの回転

(iii)視点のZ軸回りの回転

(iv)3軸回りの回転