福島県教育センター所報ふくしま「窓」　No.121（H09/1997.7） -022/042page

　任意に作り出した3つの台形の共通点を探す活動を通して、1組の向かい合う辺が平行であることを導き出させたい。調べる観点をしぼることによって、調べる内容がわかり、自信を持って結果を発表できるようにさせたい。

　(3)　実践の概要

　1　「四角形探検カード」の活用について

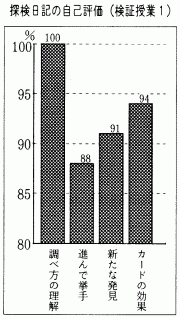
　本時の自己評価によると、右のようになり、調べる観点についての話し合いに時間がかかったがそれだけに、何について調べるのか十分にわかって調べる活動に入れたという事がわかる。

　ほとんどの児童のカードには、向かい合う一組だけ平行であることが記入された。ただ、下位児の中には、3つの図形の性質を比較して共通にいえることを探すということで頭が混乱し、一つ一つを調べることだけで精いっぱいだった子も見られた。

　一つの図形についての特徴を探すことは簡単だが、調べる対象が3つあって、その3つに共通する特徴を探すということはより高度な課題であった。そのため調べる段階の後半から苦しんだ児童も多く、全体で意見を出し合い、確かめていくことでようやく理解できた様子だった。

　当初、自己評価欄に「進んで発表したか。」という項目を入れて正方形と長方形の学習の時に使ったが、「手を挙げてもさされなかったから発表しなかった」と考えて△印を付ける子が多かったため、台形の学習の時間から「進んで手を挙げたか」という言い方に変えてみた。

　その結果自己評価欄に○印が増え、満足そうな表情が多く見られるようになった。また、回を重ねる度に挙手する児童が増え、意欲的に学習に取り組む姿が見られた。

2　「脱出カード」の活用について

　ほとんどが納得できた様子を見て脱出カードの問題に取り組ませた。平行線を使って作図する問題は全員が正解し、中にはすきまなくたくさんの台形を作った子もいた。弁別する問題では全員が正解したが、そのわけを書くところで「一組が平行だから」と答えられたのは62%だった。

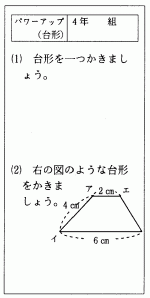
　脱出カードが終わった児童のために、「パワーアップ問題」を用意し、時間を有効に使.い、より力を伸ばすための工夫をした。問題内容は、作図で、自由にかくものと、与えられた大きさのものをかく2問とした。

　時間的に余裕があり次への意欲も旺盛で全員がパワーアップ問題に取り組んだ。自由に台形をかく問題は全員が正解し、長さや角度を与えられた問題では72%が正しくかけていた。しかし、規定された作図は初めてだったため、底辺からかかず上底からかいた子も何人かいて、だいぶ苦労していた。困った子どもたちが何人か集まって考えているところへ上位児が来て、「僕は下からかいていったらうまくいったよ。」とアドバイスしてくれ、お互いに教え合い、学び合う姿が見られた。