福島県教育センター所報ふくしま「窓」　No.128（H11/1999.11） -014/042page

【資料2】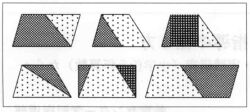

このように既習の図形の面積の求め方を生かした考え方が数多く出されたことは、毎時間図形感覚を養う手だてを行ってきたことや、前時までの平行四辺形、三角形の面積を求める学習で本時のような展開授業を実施した結果と思われる。

さらに、三角形の求積において、合同な三角形2つから平行四辺形をつくり、それを2等分することにより三角形の面積を求めるという倍積変形の考えを本時の学習でも用いた児童が数名おり、この点においても既習の考えを生かしていることが分かる。

［2］　多様な考えを引き出し、それぞれのよさを感得させる

ア　授業の実際

前述したように、既習の知識で学習課題を解決して多様な考えを引き出すようにした。

学習シートにより自力解決を行わせた。学習シートの構成は、「学習課題、台形の図（長さは示さない）、方眼上に示された台形の図、まとめ」である。図に長さを示さなかったのは、面積を求めるのに必要な長さを児童自らに見つけさせるためである。1cm方眼上に示された図から、必要な部分の長さを測らせた。さらに方眼上に示さない図を提示することにより、台形がいろいろな図形に分けられるという考えに気付きやすくした。また、問題の台形の図には辺の長さや高さを表示せずに、面積を求めるために必要な辺の長さや高さを自らの求め方に応じてそれぞれ測るということにした。

「比較検討」の場では、前述のような多様な考えが出されたが、考えの根拠を明らかにして、既習の図形求積とどのように関わっているのかなどを中心に発表させ、それぞれの考えのよさに気付かせた。

イ　考察

児童は、友達の発表を聞くことにより、多様な考えがあることに気付くことができた。ここでの学習が本時以降の学習で生かされることになると思われる。また、それぞれの考えについて教師から補足説明があった。例えば、倍積変形の考え方では、児童が発表した「（もう一つの合同な台形）があるものと考えて」という考え方をほかの児童にも分かり易いように説明する場面があった。数学的な考え方を育てるという点で効果的であった。

(2)　「割合のくらべ方と表し方」の授業

「こみぐあい」について理解し、どのような方法で異種の2つの量を比較するかをねらいとした授業での実践である。なお、本時は2時間扱いとした。

［1］　児童がつまずく言葉に配慮した指導をする―「こみぐあい」の指導―

【資料3】

ア　授業の実際

「こんでいる」、「すいている」は日常的に使っており、その様子をイメージしやすい。そこで、【資料3】の展開で行った。

児童から「こんでいる」、「すいている」とい