数直線上に｜x｜＝3を満たすxの値を表す点をかきなさい。
○左辺に絶対値に囲まれた文字,右辺に値の入る絶対値を含む方程式において,絶対値がはずれるとき,どのような計算がなされるのか数直線に指し示す。


「数直線上に｜x-3｜＝5を満たすxの値を表す点をかきなさい。

○左辺に絶対値に囲まれた文字式(1次式の多項式),右辺に値の入る絶対値を含む方程式では,「何が求まるのか」「どのように計算されるのか」を数直線を使って考えさせる。

3より右方向(正方向)では,｜x-3｜＝5　∴x-3＝5　∴x＝3+5　∴x＝8
3より左方向(負方向)では,｜x-3｜＝5　∴-(x-3)＝5　∴＝3-5　∴x＝-2
（注)｜a｜＝k⇔a＝±kを利用してx-3＝±5としてもよい。
○｜x｜が原点からの距離を表していたのに対し,｜x-3｜は座標3からの距離を表すことになる。それで「3を境目として式が変わる」と視覚的に理解させる。


（2)数直線を利用して視覚的に場合分けを理解させる。(→数Aで)
｜a｜の絶対値をはずしなさい。
○方程式｜a｜＝2を解くことと｜a｜の絶対値をはずすことの違いを明確にさせることが大切である。場合分けにより2つの値をもつようになるのではなく,｜a｜という1つの絶対値に数として1つの値が対応することを理解させる。

｜x+3｜の絶対値をはずしなさい。
○｜x-α｜の絶対値を外す場合,数直線上にαを表す点をとり,αより右方向と左方向では絶対値の外れ方が異なることを視覚的に理解させる。(下はα＝-3のとき)
また,問題によってαが変わると数直線上のどこが境目となって,外れ方が違ってくるのかを具体的に数値を代入しながらαの変化をとらえることも必要である。


｜x+2｜+｜x-5｜の絶対値をはずしなさい。
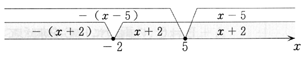
○絶対値を含む式が2つ結びついた場合,4つの場合分けを考えてしまうつまずきは多い。絶対値を外す境が2箇所になることから3つの区間に分けられることを数直線を利用して視覚的に理解させる必要がある。その上で,必要があれば関数としてグラフをかき,場合分けが3通りできることを理解させて行くことで定着を図る。