3）解を視覚的にとらえさせるために,数直線上に表す習慣を付けさせる。

4）様々な条件下で解をとらえさせる。
(例)x+4>3の解を次の中から求めよ。
ア　-2,-1,0,1,2　イ　1桁の自然数　ウ　数全体

(2)不等式の性質の指導では
1）てんびんや数直線などによる視角的操作を利用し,時間をかけて理解させる。
2）まとめの段階などに自作問題作りを取り入れると理解が深まる。
(例)A<Bとして,問題を生徒に作らせ,互いに解かせる(不等号を入れさせる)。
3）等式の性質と対比しながら,共通点,相違点を理解させる。(サクシードp14を再掲)

【等式の変形】
1）両辺に同じ数を加減できる。
2）両辺に同じ数を乗除できる。
3）AB＝0ならばA＝0またはB＝O

【不等式の変形】
1）両辺に同じ数を加減できる。
2）負の数を乗除すると不等号の向きが変わる。
3）AB>0ならば(A>0かつB>0)または(A<0かつB<0)

(3)1次不等式の解法の指導では
(→中2で)
解法の手順をアルゴリズム化してまとめる。その際,方程式の場合と比較して共通点や違いに留意して,各手順の持つ意味を理解させることが大切である。
【1次不等式の解法のアルゴリズム】
1）ax>bなどの形に整理する。
ア　分母を払う。
イ　かっこをはずす。
ウ　移項して整理する。
2）係数aで割る。(割る数の正負に注意)

(4）不等号の向きの誤り防止と高校への発展学習として,「境界点の考え」を用いてみる。
(→中2で)
境界点の考えとは,「方程式の成り立つ値が,不等式が成り立つ範囲の境界になっている」ということで,この考えは,高校の「不等式の表す領域」(数2)へと発展してつながっている。
(例)2x-3>4x+2
ア　方程式にして解き,境界点を求める。
→2x-3＝4x+2　∴　x＝-5/2
イ　不等式にOを代入して,成り立つか成り立たないかを調べる。
→2×0-3>4×0+2　これは成立しない。
ウ　不等号の向きを決定する。
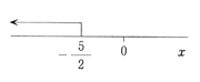
→xは-5/2を基準として
0を含まない範囲だからx>-5/2