2　つまずきの分析

(1)変域に対する理解ができていない。
日常の事象の中に1次関数を見つけて式に表すことにくらべ,変域についての理解ができていない傾向にある。原因として,変域という語が中1で出てくるが,不等号を本格的に扱う不等式は中2で学習するので,生徒にとっては理解しにくいことが考えられる。また,方程式や不等式の応用での「解の適,不適」の取り扱いが少ないように,変域を扱う問題にあまり接していないこともつまずきの原因として考えられる。

(2）y→xの対応としての逆関数的な見方は中学校ではあまり取り上げられていない。例1,例2ともに,yの変化に対応するxの変域を求めるという,逆関数としての取扱いをするため,生徒はとまどうと考えられる。

(3)xの係数aが負であるために,関数の変域がとらえにくい。
a<0のとき,xが増加するとyは減少するので,xの変域を表す不等号の向きとyの変域を表す不等号の向きとが逆になるところがよく理解されていない。
また,xの係数が負の分数なので,変域を求める際の不等式が解きにくくなっている。

3　つまずきへの対策
(1)変域につながる内容はていねいに指導しておく。(→主に中1,中2で)
変域につながってくる内容として,1,2年時で学習する不等号や方程式,不等式の解の適,不適について,ていねいに指導をしておく必要がある。

(2)xとyの対応を双方向で取り扱う機会を持つ。(→中,高ともに)
関数のグラフはx→yの対応でかくが,例1や例2のような問題を通して,y→:xの対応を意識させながら変域について考えさせる機会を持つことが必要である。

（3）xとyの変域の対応をグラフ上で視覚化して理解させる工夫をする。(→中,高ともに)
変域の範囲を的確に把握させるためには,グラフを利用して視覚的に理解させるようにし,機械的に変域の両端の値を代入して求めるだけということにならないように注意する必要がある。このことは,単調関数でない「2乗に比例する関数」(中3)や高校で扱う種々の関数の変域を考える際に大きな影響が出てくる。

【例2のグラフによる求め方】

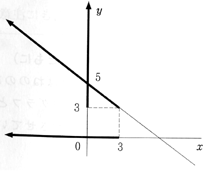
【y→xの対応】
y≧3は,y軸ではどのような範囲か。
　　　　　↓
そのときのグラフの範囲はどうか。
　　　　　↓
そのときx軸ではxの範囲はどうか。