平方完成をする際に,中学校では「方程式の両辺に平方数を加える」という方法をとるに対して,高校では,「式の変形の過程で平方数を加えて引く」という方法をとる。このように中学校と高校では平方完成の過程に2つの異質な要素がありつまずきが生じやすい。

(3)中学校における2次式の平方完成の扱いは解の公式を導くまでが主である。
中学校における2次式の平方完成は,3年で学習する「2次方程式の解の公式」を導きだすための前段階として,「平方根の考えを使って解く」として扱われている。しかし,この解法は直後に学習する解の公式に吸収されて,2次方程式の解法は因数分解による方法とや解の公式の利用に重点が置かれることから,平方完成は次第に忘れられ,結果としてなかなか定着していない。


3　つまずきへの対策
(1）面積図を利用して平方完成を理解させる。(→中,高ともに)
1）乗法公式を理解させ,その逆演算として,因数分解の理解を深める。
乗法公式(x+a)2＝x2+2ax+a2
　　　　(x-a)2＝x2-2ax+a2

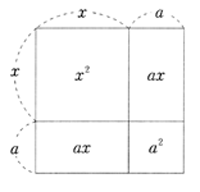
2）さらに,具体例を通してイメージを定着させ,平方完成につなげる。
(例)x2+6x＝(x+3)2-32

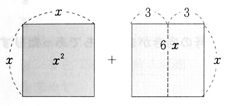
(3は6の半分)
↓

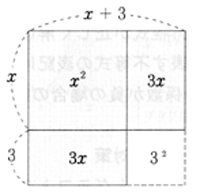
(2)中学校の平方根の考えによる2次方程式の解法を復習した上で,方程式の変形と式変形の違いを意識させて,段階を踏みながら平方完成を指導する。(→数1で)
　
【方程式の変形の考えを利用した段階的な平方完成の指導】
1）y＝x2+ax→2）y＝ax2+bx→3）y＝ax2+bx+c
1）ア　xの係数が偶数のとき,y＝x2+2・a'xと変形して,両辺に(a')2を加える。
イ　xの係数が奇数のとき,y＝x2+ax＝x2+2・a/2xとして,偶数の場合に戻る。
2）x2の係数が1でないとき,両辺をaで割り,y/a＝x2+b/axとして,1）に戻る。
3）定数項がついているとき,y-c＝ax2+bxと移項して,2）に戻る。