(2)2次不等式の意味と解法をグラフとの関連でパターン化して,一貫した指導をする。

【パターン】
不等式の左辺を関数としてとらえる
　　　　↓
y＝0とおいた2次方程式を解く
　　　　↓
グラフからy＞0となるxの値の範囲を読み取る

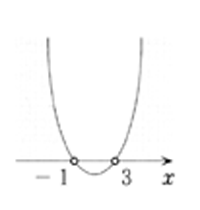
1）グラフがx軸と2点で交わる場合
x2-2x-3＞0
(x+1)(x-3)＞0
y＝(x+1)(x-3)とおき
y＝0とすると,x＝-1,3
右図から,y＞0となるxの値の範囲を求めて,
x＜-1,3＜x
y＞0
y＝0
y＜0
左辺を関数としてとらえる
　　　　　↓
y＝0の2次方程式を解く
　　　　　↓
グラフからy＞0となるxの値の範囲を読みとる

※2次方程式を正しく解くことを確認する。※〜を強調する。※解答の表記は,グラフに合わせたこの形が望ましい。

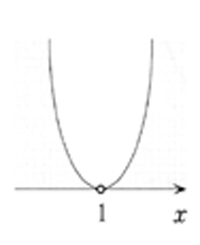
2）グラフがx軸と接する場合
x2-2x+1＞0
(x-1)2＞0
y＝(x-1)2とおき
y＝0とすると,x＝1
右図から,y＞0となるxの値の範囲を求めて,1以外のすべての数
y＞0
y＝0
y＜0
左辺を関数としてとらえる
　　　　　↓
y＝0の2次方程式を解く
　　　　　↓
グラフからy＞0となるxの値の範囲を読みとる

3）グラフがx軸と共有点をもたない場合
2）と同様に考えて,すべての実数。
(3）グラフとの関連を考えさせて,いろいろな形の問題演習を行う。(→高校で)
(練習)次の2次不等式を解きなさい。(難易順は1から10になるにつれて難しくなる)
1）(x+2)(x-6)≦0(難易順1)　2）x2-2x+1＞0(難易順6)
3）x2-3x≧0(難易順3)　　　4）x2-3x+5＞0(難易順8)
5）x2-4x+1＞0(難易順2)　　6）2x2-x+1＜0(難易順4)
7）-x2+x+2＜0(難易順7)　　8）9x2+6x+1≦0(難易順5)
9）1-4x＜4x2(難易順9)　　10）3x-2x2≦6(難易順10)