6　文字定数を含む場合の2次関数の最大・最小(数1「2次関数」)
関連:前　中学校では扱わない　後　絶対値(数A),三角比の値(数1)

1　つまずきの内容
高校1年の数学は,数学の2次関数で始まることが多いが,2次関数の発展的な内容である文字定数を含む場合の最大最小は,多くの生徒にとって,つまずきやすい内容である。具体的には,次のような問題である。

2次関数y＝x2-2ax(a＞0)の2≦x≦4における最小値を求めよ。
解)y＝(x-a)2-a2……1）
より,軸の方程式は,x＝aである。
(1)0＜a＜2のときx＝2のとき最小で最小値は,4-4a
左端で最小

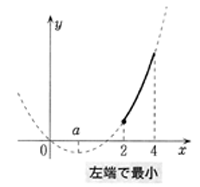
(2)2≦a＜4のときx＝aのとき最小で最小値は,-a2
頂点で最小

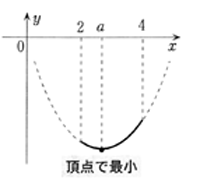
(3)4≦aのときx＝4のとき最小で最小値は,16-8a
右端で最小
(1),(2),(3)より,求める最小値は
0＜a＜2のとき4-4a
2≦a＜4のとき-a2　　　　｝（答）
4≦aのとき　16-8a

「軸の方程式x＝aのaの値によって場合分けして答える」のがポイントであるが,

1）場合分けとは何なのかがわからない。
(xが変数なのに,aの値もなぜ変わるのかがわからない。)

2）なぜ軸の値で場合分けしなければならないのかわからない。

3）どのように場合分けすればよいのかがわからない。

というようなことが,生徒にとっての疑問点である。
このことは,数学Aの数と式の内容である「絶対値の場合分け」にも,共通して言えそうである。