サクシード2中学校数学から高等学校数学へ-048/69page
3 つまずきへの対策
(1)定義と定理(公式)の区別を明確にさせる。(→中,高ともに)
sinAは=y/rは「こう決める」という定義であり,a/sinA=b/sinB=c/sinC=2Rのような「定義から導かれた事実である定理」とは異なることを理解させる。
(2)鈍角に三角比を拡張した「よさ」と学ぶ意義を理解させる。(→数1で)
鋭角の三角比を定義し,活用することにより,三角形において角度と辺の長さを同時に扱うことができるようになったが,さらに鈍角に角を拡張して三角比を定義する(定義の拡張)ことにより,あらゆる三角形で,直接測定することが困難な距離,高さ,面積などが求められるという「よさ」を獲得したことを理解させる。
(3)三角比の定義の指導例
1)鋭角の三角比の場合
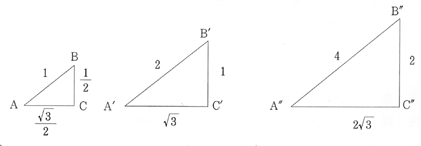
(1)3つの三角形が「相似」であることを確認させる。
BC:AB:AC=B'C':A'B':A'C'=B"C":A"B":A"C"
(2)3つの三角形において,例えば,隣辺と対辺の比はすべて等しいことを示し,三角比の定義として適当であることを確認させる。
BC/AC=B'C'/A'C'=B"C"/A"C"=1/√3=tan30°
(3)1:2:√3=1/2:1:√3/2のように,斜辺(半径)が1の場合の30°,45°などの3辺の比を,図を通して理解させ,定着を図る。
2)鈍角の三角比の場合
鈍角の場合は直角三角形ができないので,鋭角で定義したtanA=y/xのy/xなどを座標に読み替えて,直角三角形から離れた一般化をしていることを理解させる。
便宜的に,次のような1辺の長さが負の三角形を考えると,鋭角との場合との接続が図りやすい。
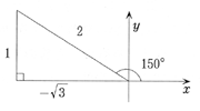
tan150°=1/-√3
Copyright (C) 2000-2001Fukushima Prefectural Board of
Education All rights reserved.
掲載情報の著作権は福島県教育委員会に帰属します。