3）0°,90°,180°の三角比の場合
例えば,O°の場合,図のような三角形を考え,∠Aが0°に近づくと,BCは、0に近づくから,sin0°＝0/AB＝0と考えられ,y＝0の場合の定義と一致する。
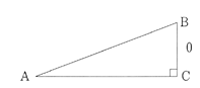←イメージをつかむため0と書いてみる。

4）三角比の定義を座標平面で考えること
上記1）2）3）等の方法で理解させたとしても,最終的には座標平面を活用した定義を繰り返し指導し定着させたい。その際,例えば,sinθ＝y/rと文字のみで表現するばかりではなく,sinθ＝y座標/半径と言葉で意味づけして,具体的なイメージがつかめるようにすることも大切である。

(4)三角比を定義する際心がけたいこと
1）三角比の導入の順序に配慮する。
指導する側からみると教科書を進める上では,sinθ,cosθ,tanθを一度に定義した方がまとまりがよく,進度も速くなるが,生徒にとっては,3つ一緒では混乱を招きやすい。一般には,一度に定義せず,tanθの意味を理解し活用できるように指導した後でsinθとcosθを指導したほうが無理がないようである。

2）特殊な角の三角比の表の作成と活用を図る。
O°≦θ≦180°の三角比をひと通り学習した後で,sinなら次のような表を作成し,三角比の値の特徴を視覚的にとらえさせ,様々な公式を導く手がかりとする。

	0°	30°	45°	60°	90°	120°	135°	150°	180°
sinθ	0	1/2	1/√2	√3/2	1	√3/2	1/√2	1/2	0

表の,sin30°＝sin150°などの対称性から,sin(180°-θ)＝sinθなど

3）「長さ」と「比」を区別した表記法に心がける。
「長さ」

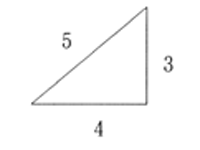
「比」:丸数字を活用