理科学習指導資料高等学校「理科2」の指導-022/139page

図6

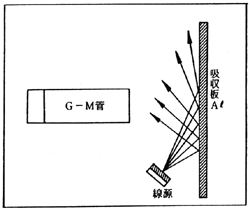
(6)γrayの吸収を調べ,吸収係数を求めてみる。
　 ここで用いる G―M管は,ガラス窓のものでよい。他の放射線に比べて,γ線は物質と相互作用を起す確率が低く,相互作用を起し,吸収されるプロセスは a,β粒子とは異なる。
　 γ粒子の一部は吸収,散乱されるが,大部分は通過し,その減弱は指数関数に依ることがわかっている。
　 全てのγ線で,エネルギーを一定にそろえ(単色放射線)コリメートした線束であれば,次の式で示される。
　　　強さ　I＝I₀e^−μx　(I ：厚さ x における強さ, I₀ ：厚さ0のときの強さ,μ：線減弱係数〔cm⁻¹〕)
この式は,光の吸収係数の式と全く同じである。

　1) G―M管とγ線源を 5〜7cm 位離し,その間の吸収板 (pb) の厚さを変えて測定する。なお,厚くなると計数が少なくなるので,計測時間を長くするとよい。
　 バックグラウンドを差し引かなければならないので,この計測もきちんとする必要がある。
　2)データを表にし,バックグラウンドを差し引き,グラフのように片対数のグラフに処理する。(図7)
　3)線減弱係数μを求めてみよう。初めの放射線の強さを 1/2 にするのに必要な pb の厚さがわかれば次の式で線減弱係数μを求めることができる。但しρは Pb の密度である。
　　　∴μ＝0.693ρ/X _1/2

図7

(7)γrayによる逆2乗則について調べる。
　 γrayは他の電磁放射と同様逆 2乗則が成立する。
　 線源は大きさがあるし,周囲の物質からの散乱もあり,バックグラウンドもあるので,こうした影響による計数を差し引くことにより,比較的一致したデータが得られる。
　　　I＝k/d² (I ：測定値)＝k/(D＋x)²　(D ：線源から G―M管上の一点までの距離, x：補正項)
　 上式より計測した I を表にし, D＋x＝d でグラフにより補正をすれば関係が求められる。G―M管と線源の距離Dは 8cm〜40cm の間でいろいろ変化させて求めればよい。

4　考察

　 3の方法のうち,いくつかを実験し,考察しよう。
　 また,(6)のグラフ(図7)に表わされるような関係は,自然界に数多い現象としてみられる。光以外では,横軸を時間にするコンデンサーの放電曲線,放射能半減期,心理学では忘却曲線などが興味深い。