研究紀要第6号 学習指導改善に関する研究 理科実験 - 026/036page

要がある。これには二つの方法があり，一つは偏差の割合による方法，もう一つはｘ²（カイ2乗）法である。

（1）　偏差と平均誤差による方法

偏差（D）……実験値と理論値の差

（Nは総個体数，Pはある表現型の現れる確率ｑ（1-ｐ）はその表現型の現れない確率）Dとmを比較して，Dがmの3倍以内であるときは，この偏差は誤差の範囲内である。すなわち実験値は理論どおり分離をしていると判定する。

単性雑種の場合を検定してみると

表現型	工常翅	痕跡翅	計
実験値	357	124	481
理論比	361	120	481
偏差（±）	4	4

平均偏差を求めてみると

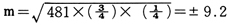
以上のことから，この実験比は3:1の理論比に一致しているとみなす。

両性雑種の場合を検定してみると

表現型	++	+e	Vｇ+	vge	計
実験値	533	168	170	56	927
理論値	521	174	174	58	927
偏差（±）	12	6	4	2

各平均偏差を求めると
12＜15．1ｘ3
6＜11．8ｘ3
4＜11．8＜3
2＜7．4＜3

いずれの場合も，Dはmの3倍より小さいので，実験比は9:3:3:1の理論比に一致するとみなして差支えない。

2.ｘ²による方法（chisquare　test）

前法より確実で，この方法の方が最近よく用いられ，特に不連続量である場合，帰無仮説がデーターによって支持されるかどうかをみる。

このようにして求めたｘ²の値が，．（P＞0．05）の場合は帰無仮説を捨てることができない。すなわち，仮説に反していないと考え，それは単なる誤差と見なし，（(P＜0.05）の場合は，仮説は捨てられ，データーは理論に反して有意の差であると判断する。この場合の帰無仮説は「実験値は理論通り3:1，9:3:3:1に分離している」と立てたものである。なお自由度は階級値の数より1を引いた値で表わす。

単性雑種の場合をこの方法で検定してみると
0．177<3．841

²の値は0．05のときより小さい，すなわちP（適合確率）は0．05以上の値を示すので，理論値と一致しているとみなして差支えないことになる。

両性雑種の場合を検定してみると

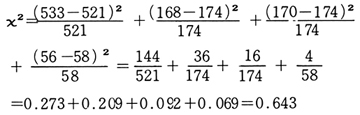
この場合，自由度は4-1=3であるのでｘ²分布 表より照し合せると，有意水準の値が7．815であり0．643は7．815より小さいから，この実験値の差は有意の差でないことになる。

　　x²の分布表

◆表の濃淡は帰無仮説をすてるべきであるという程度に濃くなり，Pが0．05以下であるとき一般に仮説は捨てられる。