研究紀要27号 児童・生徒の学習能力の発達 - 037/082page

算数としての形式にとらわれることなく，児童の自主的で自由な考えを大くとり入れ，アイディアも大切にしていきたい。

◎教師は計画に強くしばられた授業を展開しないようにする。これは必要に応じ，本時の授業の流れに対応できるような幅をもって，教師と児童の学習上のコミュニケーションを深めたいものである。

　

3．指導の実際

（1）　単元名小数　　　　　（2）― 小数のかけ算

（2）　概　観

�@　題材観

　3学年では，測定値の端数部分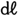（の端数など）を表す数として，1/10の位までの小数を導入し，これを用いて小数のしくみや加減算について学習している。
　その上にたって4学年では，「小数（1）」で小数を1/1000の位まで拡張し，小数を抽象数として認めることができるようにすることを重要なねらいとして指導してきた。

　また，小数の単位と相対的な大きさ，大小比較，小数の表し方が整数と全く同じしくみになっていることなどの理解を深めながら抽象数として認められるようにもしてきた。
　小数の加減算については，「小数についても加減算ができることをおさえ，1/10の位までの数について簡単な場合の加減算の指導がなされている」ことをうけて，これらの理解の上で，小数第3位までの加減算を学習してきている。

　そこで，本単元では，今までの小数の理解のうえにたって，整数どうしの乗除と同じように，小数×整数，小数÷整数の乗除算と整数÷整数（商が小数）などの演算方式を学びとり，小数の数としての理解をよりいっそう深める単元である。
　本単元は，次の二つの小単元から成り立っている。すなわち，第1小単元「小数のかけ算」，第2小単元「小数のわり算」の2つである。（東書，新しい算数4下の単元構成）

第1小単元　　「小数のかけ算」

　この小単元は，小数×整数の演算方式を理解させる単元である。（小数は，第1位から第3位まで，整数は，1位数から3位数まで）その内容としては，次のようなものである。

小数第1位の数	×	整数1位数
小数第1位の数	×	整数2位数
小数第1位の数	×	整数3位数
小数第2位の数	×	整数1位数
小数第2位の数	×	整数2位数
小数第2位の数	×	整数3位数
小数第3位の数	×	整数1位数
小数第3位の数	×	整数2位数
小数第3位の数	×	整数3位数

　これらの演算方式を理解させるため，はじめに，小数第1位の数×整数1位数を事実算を考えさせることにより，小数×整数の演算の基本型の意味を理解させることから導入していく。

　乗法関係については，整数の場合は，ほとんど理解されているから，数が整数から小数へと拡張されたこととあいまって乗法の意味づけを正しく行うことが重要であり，乗法の意味を理解させることが第1歩となる。小数の乗法は，基本的には，小数を整数化して整数計算に還元し，その結果をもとの小数の単