位でとらえることが原則であるので,「給食のスープを1人に0.2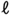 ずつ配ると7人ぷんでは,何
ずつ配ると7人ぷんでは,何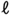 いるでしょうか。」(東書 4年下P56の問題)という測定量を導入例として
いるでしょうか。」(東書 4年下P56の問題)という測定量を導入例として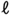 を
を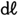 に換算して,2×7と整数化させ14
に換算して,2×7と整数化させ14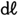 をもとの単位に換算すると1.4
をもとの単位に換算すると1.4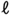 になる。この整数化してのかけ算やさらに能力の低い子の発想を助けるための累加の方法(0.2
になる。この整数化してのかけ算やさらに能力の低い子の発想を助けるための累加の方法(0.2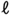 を7回たして1.4
を7回たして1.4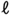 になる)などから1.4
になる)などから1.4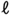 という全体量を求めることにより,
という全体量を求めることにより,
0.2×7=1.4
の演算方式を
ア、0.2と7を上下に書き,整数のかけ算と同じように計算する。
イ、かけられる数は,小数点の右1けたあるから,積も小数点の右に1けたあるように小数点をうつ。
というふうに一般化する。
この一般化したことをもとにして,乗数が2位数,3位数になった場合を考えさせ,乗数が2位数,3位数になっても,演算方式には,かわりないことに気づかせる。
さらに,被乗数が,小数第2位の数,第3位の数になった場合,再度,測定量にもどして,計算方法の確かめをしながら,小数×整数の計算方式をまとめていくものである。
指導の例は,「小数のかけ算」についてとり扱うので略す。
② 児童観
この単元を指導するにあたって,児童に必要と思われる能力を
ア、整数どうしの乗法の演算力
イ、小数についての理解状況
ウ、問題の処理態度や発言力
の3点から考えて次のような調査をした。
(児童数20名)
なお,ウは,授業の観察によってまとめたものである。
|
観点
|
項目
|
内容
|
結果
|
考察
|
|
ア
・
整
数
ど
う
し
の
乗
法
|
2位数×1位数
|
|
○……20 |
すでに学習した内容だが問題点がいろいろとみられた。
○くり上りをたさないでいる者がいる。
○空位のあるかけざんが不正確。
○けた数がふえると定着度がおちる。
○特に乗数が3位数になると著しくなる。
○やり方を忘れていた者が3人ほどいた。
○かけざん九九のまちがいがみられた。
・7×5=32
・7×5=30
・3×8=27
・2×7=16
○かけざん九九を全部書かせたときにはまちがいがなかった。
○計算に対する落ち着きがないのと練習量が少ないのが原因と思われる。
|
|
3位数×1位数
|
|
○……17
×……3
(くり上げ忘れ
400とした) |
|
4位数×1位数
|
|
○……19
×……1 |
|
1位数×2位数
|
|
○……18
×……2
(かけざん九九
7×5=32
7×5=30) |
|
2位数×2位数
|
|
○……19
×……1
(くり上げ忘れ) |
|
3位数×2位数
|
|
○……19
×……1
(くり上り忘れ) |
|
1位数×3位数
|
|
○……18
×……12
(くり上り忘れ) |
|
2位数×3位数
|
|
○……11
×……9
(くり上げ忘れ 5
九九ちがい 5) |
|
3位数×3位数
|
|
○……12
×……8 |
|
イ
・
小
数
に
つ
い
て
の
理
解
|
小数に対する理解 |
整数は小数といえる |
いえる……5
いえない……15 |
小数に対する意識は。まだまだ子どもの中には定着していない。
「小数(1)」のときにはかなり小数の大きさについて指導したが不完全である。
小数の第1位より第3位にいくに従って理解が浅い。
単位の換算は,測定量を考えるときに必要なのだが小数第1位数より第3位の数との換算(㎞-m ㎏-g)がよくない。 |
| 小数は0より大きいか小さいか |
大きい……12
小さい……8 |
| 0.03と0はどららが大きいか |
0……7
0.03……13 |
| 1は0.1がいくつ |
10……19
1000……1 |
| 単位の換算 |
13.5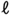 は何 は何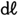 |
135……16
13.5……2
1.35……1
0.135……1 |
| 43㎝は何m |
0.43……16
43……3
430……1 |
| 1㎞326mは何㎞ |
1.326……16
1326……3
1㎞326m……1 |
| 3.81㎏は何g |
3810……5
381……12
0.381……1
3081……1
3.810……1 |
ずつ配ると7人ぷんでは,何
いるでしょうか。」(東書 4年下P56の問題)という測定量を導入例として
を
に換算して,2×7と整数化させ14
をもとの単位に換算すると1.4
になる。この整数化してのかけ算やさらに能力の低い子の発想を助けるための累加の方法(0.2
を7回たして1.4
になる)などから1.4
という全体量を求めることにより,
は何