尭偟側偄傛偆偵搘傔偨丅
5丏峫丂丂嶡
丂偙偺彫悢亊惍悢偲偄偆4擭惗偺彫扨尦傪
仜丂帣摱偺敪憐傗巚峫偺棳傟傪偩偄偠偵偟偰巜摫偡傞丅
仜丂帣摱偨偪偵墘嶼宍幃傪尒偮偗偝偣掕拝傪偼偐傞丅
仜丂4帪娫偺拞偱栤戣揰傪惓偟偰偄偔丅
仜丂帣摱偨偪偺尒偮偗偨嶼朄傪惗偐偡丅 |
|
|
|
偲偄偆娤揰偐傜巜摫偟偰偒偨婰榐偱偁傞偑丆偙偺婰榐偐傜丆寢榑偲偄偆傛偆側抐尵偡傞傕偺偑偁傞偐偳偆偐丆傑偨丆尵偭偰傛偄偐偳偆偐媈栤偱偁傞丅
丂偦傟偵丆1妛媺偩偗乮嬐偐20恖偺妛媺乯偱丆専徹傕側偟偺庼嬈偩偗偵丆偦偺晄埨傕嫮偔巆傞丅
丂嘆丂巜摫寁夋偲帣摱偺斀墳
丂偙偺彫扨尦偺巜摫帪娫傪4帪娫偲偟乮偆偪丆傑偲傔1帪娫傪娷傓乺帣摱偺巚峫偺棳傟傪拞怱偵偡偊偰巜摫偵偁偨偭偰偒偨偑丆帣摱偼丆梊憐奜偵妶摦偟偰偔傟偨丅乮敪尵傗巚峫偼憤偠偰掅師尦偩偭偨偑乯
仜丂恎嬤側栤戣偐傜偼偄偭偨偨傔丆帣摱偺敪憐偑丆椵壛偲偄偆堄枴偵偍偪偮偄偨偙偲偼丆帺桼側峫偊偱夝偔乮挷傋傞抜奒乯偵敪揥偟傗偡偐偭偨丅
仜丂帣摱偺帺桼側夝偒曽偱偼丆偙偺椵壛偑懡偔偺巕偵巊傢傟傞偐偲巚傢傟偨偑丆梊憐傛傝偼彮側偐偭偨丅
丂傑偨丆2亊7偲偄偆扨埵偺姺嶼傪偟偰寁嶼偡傞巕傕梊憐傛傝傕彮側偐偭偨丅偟偐偟丆0丏2亊7偲偄偆寁嶼傪偟側偑傜丆摢偱偼丆2亊7偲偄偆姺嶼偺奣擮傪傆傑偊偰偄偨傛偆偵巚偊傞丅乮戞1帪丂傒偮偗傞抜奒偱偺C6偺敪尵嶲徠乯
仜丂偙偺応崌偺巕偳傕偺堄幆偼丆彫悢偺壛朄偲忔朄偑堦懱偲側偭偰偄傞偲偄偊傞丅
| 丂 0丏2亊7=0丏2亄0丏2乧乧乧亄0丏2=1丏4偩偐傜彫悢揰傪傑偭偡偖偍傠偡丅
丂丂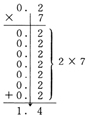
|
丂偙傟傪
乽彫悢乮0丏2乯傪惍悢乮2乯偵偟偰丆偐偗丆愊乮14乯偺扨埵傪娨尦偟偰丆彫悢揰傪偆偮乮1丏4乯乿
丂偲偄偆寁嶼曽朄偱偼丆庤娫偑偐偐傝丆偍偦偔側傞傛偆偵巚偊偨傜偟偄丅偙傟偼崱傑偱偺巜摫偺寚揰偑偁傜傢傟偰偒偨偲傕偄偊傞丅偦傟偼丆傒偮偗傞抜奒偱丆巕偳傕偨偪偵丆寁嶼曽朄偺敪尒偺偒傔偰偼乽憗偔丆惓偟偔乿偲偄偆娤揰偩偭偨偐傜偱偁傞丅
仜丂彫悢x惍悢傕丆偙傟傪昅嶼宍幃偵偟偨偑偭偰峴偆偩偗偱偼丆峫偊偨偙偲偵偼丆側傜側偄丅
仜丂巜摫偺婰榐偺拞偱傕弎傋偨偑丆戞1帪偺傑偲傔偱丆杮帪偺乽惍悢乮偐偗傞悢乯偑丆2埵悢丆3埵悢偵側偭偨応崌乿傕摨偠傛偆偵寁嶼偡傞丅偲偄偆偙偲傪巜摫偡傟偽丆偐傫偨傫偵偡傓偙偲偱偁傞偑丆偦傟偱偼丆偳偆偟偰摨偠側偺偐丅1帪偺傑偲傔偲師帪偺梊崘偲偺娭楢偼偳偆偁傞傋偒側偺偐丅乮嫵巘懁偺栤戣乯側偳偑晄柧偵側傞偨傔丆偁偊偰丆偙偆偄偆抜奒傪愝掕偟偨丅
仜丂偟偐偟丆偙偺栤戣偵偁傞幃乮2丏4亊538丏2亊231乯傪偳偆寁嶼偡傞偐偲偄偆偙偲傪乽0丏2亊7偲摨偠偐乿偲偄偆栤偄偐偗偱偼丆堄枴偑傢偐傝偵偔偐偭偨傛