うに思える。その混乱は,予想として,「ちがう」といった子の中にも「計算が2だんになるから(0.2×7とは)ちがう。」という考え方を示したものがいたように,「ちがう」の意味が教師の「かけざんのしかたは,2けたかけても3けたかけても,1けたとかわりはないか」というものに対する「同じ」「ちがう」とちがっていたわけである。
これは,
●問題文の吟味をする。
●児童が,ことばからどういうイメージをうけるかよくつかむ。
●前時のまとめ(次時の問題点)を本時の問題文にどうつなぐか考える。
などから解決をはかることができると思える。
○ この時間におけるもう一つの成果は,C3が「常識的に考えると答えが,おかしいかおかしくないかわかる。」という考えを述べたことである。
このことは,答えが,いくらになっても平気でいたこの子たちに,また,いくら答えをたしかめなさい,といって見直させても,自分の考えがチェックできなかった子どもたちに一つの方向性を与えてくれた。
それは,第3時のしらべる段階に,次のような形になってあらわれた。
|
|
| 1mの重さが,1.312kgの鉄のぼうがあります。この鉄ぼう6mの重さは何kgでしょうか。 |
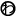 1m1.312kgを6m 1m1.312kgを6m
 6mではいくら(kg) 6mではいくら(kg)
 7.872kg 7.872kg
 |
|
1 |
3 |
1 |
2 |
|
|
1 |
. |
3 |
1 |
2 |
| |
× |
|
|
|
6 |
|
× |
|
|
|
|
6 |
| |
|
|
|
| |
|
7
|
8 |
7 |
2 |
|
|
7 |
. |
8 |
7 |
2 |
| |
|
↓
|
|
|
|
|
|
|
|
| |
|
7. |
8 |
7 |
2 |
|
|
|
|
|
|
|
|
①1×6=6なので,それに0.312があるので7になってもおかしくない
②せい数でやっても7.872になるから
|
|
①と②は今まで書かなかったことである。
そのためには,
たとえば,
| 8えんのけしゴム1こと9えんのえんぴつ1本かいました。なんえんはらえばよいでしょう。 |
(1年 ― くり上りのあるたし算より)
|
という問題を提示し,「何算でやればよいでしょう。」と聞いたとすると,子どもたちは,「はらうんだからひき算です。」と教師の8+9という予想をうらぎった答えを出す。(事実1年の授業研究に見られた反応である。これは,子どもの意識にすれば,はらうんだから,持っているお金からひくという考えは当然かもしれない。) これは,問題を読ませ,「なにざんになりますか。」(どん式が立ちますかでも)という直線的な運ぴ方をすることから,おこることである。
そこまで行かなくても,問題を読みわかること,もとめることを児童に出させ(これは,2,3回訓練することによりできるようになる。)立式に行くと図で解くのが得意な子(いわゆる線分図とか,テープ図とか,面積図とかいうものでなく自分の考えをまとめるために書く図)は,指導からとりのこされることにもなりかねないし,すくなくとも,式を立てないのだから「どんな立式」という話し合いには参加できなくなる。
さて,問題の条件をとらえさせたら,
1m1.312kgを6m
6mではいくら(kg)
7.872kg