研究紀要第33号 学習指導に関する研究 - 030/092page

�A　偶点，奇点の区別とそれらの特徴（性質）を整理すること。
　（一筆ができるものとできないものの判別，できることの原理（理由）の解明）
−位相的な図形の性質の調べ方−

　有名な“ケーニヒスベルグの橋渡し"（前頁の図）では，すべての橋をくり返さないで渡れるかどうかでなく，むしろ，位相変換によって点と線の線状図形（network）として考えることに帰着できるという数学的アイディアのすばらしさを感得させることに大きなねらいがあろう。この第一の段階をすぎてから，一筆がきができるかどうかを追求していくことになる。

　このことはまた，オイラーの多面体定理においても同じことがいえます。この定理では，公式f−e＋v＝2　を覚えさせ，これを活用することに主眼をおくことは中学生には意味がなかろう。もっと大事なことは，3次元のものを2次元に変換して考えることができるという数学的アイディアの良さを強調していくことにあります。
　このように，1つの教材には，教えることと考えさせることが数多く包含されているものです。

どこをどのように考えさせるか，どこをどのように教えるかは，指導する教師の力に負うところが多いことはいうまでもありません。
　さて，一筆がきでは，�Aにのべたように一筆がきできるかどうかの判別ができるようになってから，一筆がきできることの原理を解明していくために生徒に思考場面を設定してやることができます。原理を解明させるためには，そのことを視覚化し，単純化することが最も大切です。
　次に1つの方法をのべてみよう。

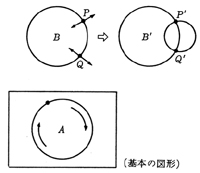
　一筆がきのできる第一の場合（偶点だけのとき）は，輪ゴムの原理であります。
　たくさんの輪ゴムを，紙の上にバラバラと置いたとき（右上図），この線上図形はいつでも一筆がきができます。
　接するとき，あるいは交わるときもあろうが，そのことには関係ありません。また，輪ゴムの数にも影響されません。
　このことを実際に確かめさせながら，原理を追求していく手法をとっていきます。

●輪ゴムをアトランダムに重ねる

　さて，輪ゴムのように偶頂点だけでできているオイラー・グラフとはどのような順序でつくられることが可能かを考えていくことにする。
　初めは，図Aのようなジョルダンの閉曲線から始める。これが，奇頂点のないもっとも簡単なグラフだからである。