研究紀要第33号 学習指導に関する研究 - 031/092page

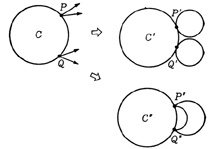
　次に，図Bで頂点Pをつくるが，それは偶点でなければならないから，もっとも簡単にPから2本の線が出るとする。この2本の線は出っぱなしでは困る（つまり奇点ができてしまうから）。当然いま1つQ点を設定し，そこからも2本を出す。
それらを無事につないでB'のようにする。B'が一筆でかけることはすぐわかる。
　また，CのようにPやQが大きな円の外側（あるいは内側）に2本がとびだすことも考えられる。

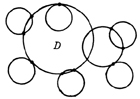
このようなことをくり返すことによりDのような場合も考えられるが，B'やC'の方法をくり返すことによって一筆がきが可能であることはわかる。

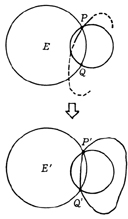
さらに，Eのような場合でもE'のようにすればよいわけで，P点にもっともたくさんの円周がかさなっても，まったく同じになる。

　次に奇点が2つの場合について考える。これはたくさんの輪ゴムの群の中に，1本のひもを置いたのと同じである。ひもの端は端点かもしれないし，ゴムの一辺につながっていることもあろうし，交点上にくるかもしれない。
　いずれにしろ，ひもの端から始め，ゴムの交点に来たら，そこでひもからはずれて，もっぱら輪ゴムをめぐりめぐってまわりつくし，再びその交点に戻ったら改めてひもの上を他端に向って進む。
このようにして一筆がきができることがわかる。

（基本の図形）