研究紀要第33号 学習指導に関する研究 - 032/092page

　以上にのべたことは厳密な証明ではないが，原理を理解させるには十分であろう。この考えのユニークさは，基本の図形として円（閉曲線）をとりだしたところにある。一筆がきという複雑な図形の考えを，日常よくみかける輪ゴムにおきかえ，ここから原理を導き出すようにすれば，生徒の解決意欲も喚起できようし，思考させる場面を設定することも可能になってくる。

　単に，一筆がきができる場合はどんなときか，といった設問で生徒に考えさせることは，試行錯誤をさせるにとどまることを知っておくことが必要であろう。
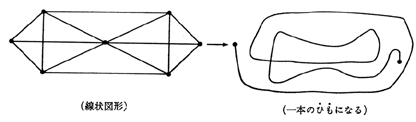
　ついでにのべると，一筆がきができるということは，観点をかえてみると，「一本のひもにのばすことができる」ことを意味している。（下図参照）

解法のテクニックを教えるのでなく，核になる考えを教えて発展できるようにさせ，将来その考えを生かして新しいものを解決できるようにさせなければならないといわれていますが，核になる考えとはどんなものをいうのですか?

　ともするとわたしたちは，問題を解く方法，つまり解法のテクニックのみを指導してそれで十分であるように思いがちです。問題が解ければよいという考えから，テクニックを教えていくことは，数多くの問題にいかにしてとりくませるか，あるいはいかに訓練してやるかの考えのみにうばわれ，本来の数学教育のねらいからはずれた指導になる危険性があります。

　解法を指導するにあたっては，その解法を支えている核になる考えはなにかをきめだしてみて，他に転移させたり発展させたりできるような指導を心がけねばなりません。
　そのためには，自分で知っている解法がなぜ有効なのかをふりかえってみて，それを支えている核になる考えを素朴な形でとりだすことに努力していくことが大切になってきます。

〔例〕　線対称移動の利用（周の長さを最小にする問題）
（問）
　図のように，鋭角BOC内の定点Pを頂点として，直線，m上に2点Q，Rをとり，周囲が最小となる△PQRを作図するにはどのようにすればよいか。