研究紀要第33号 学習指導に関する研究 - 034/092page

　さてこの問題を与えられたとき，生徒はどんな考えを頭の中で働かせるものであろうか。
　直観的に解法のひらめいた生徒は別として，解法の浮かんでこない生徒にとっては一歩も先に進めないであろう。教材としては1年でとりあげることになるが，非常に高度な問題である。
　この問題を解こうとするとき，もっとも基本となり核となる素朴な考えは，
�@　最小かどうかは，他のものと比較することによって決定できる。
�A　長さどうしは，1本の線にして比べる。
である。
とすると，�@の考えのもとに，問題はのように改題することができる。

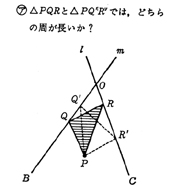
2つの三角形の周の長さはこのままでは比べることができないから，�Aの考えをもとにしての場面に解決の視点を集中させることができる。
　つまり周の長さが折れ線という比べやすいものに転換させることができた。ここで核になる数学上の知識は，"線対象移動によっても長さは変らない"という性質である。

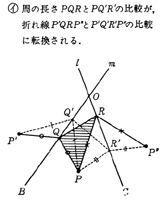
　において，どちらの線分が長いという結論を出すことはできない。にもっていくためのふくせんにすぎない。2つの折れ線がともにP'とP"をとおるということに着眼できればよいわけである。
このことから，どんな三角形のときでも2点P'とP"をとおることが推理できよう。