研究紀要第51号 「学習指導の個別化 個に応ずる研究」 -019/080page

［3］　授業の実際

ア　数学科学習指導案

昭和57年11月4日　第5校時
第1学年7組（視聴覚教室）
指導者　福島市立福島第三中学校教諭　和光幸男

1　研究主題　「個に応ずる研究」 ―個の確かな学習の成立をめざして― 本研究は，これまでの「個を認める」，「個を生かす」研究の成果をふまえた上で，教科の特質を考え，個の確かな学習の成立を目指し，一人一人の生徒が，単元あるいは毎時間のめあてを知り，授業の中での自己のつまずきや到達度をはっきりおさえ，個に応じた学習を進めることができるようにするための手だてや働きかけなど，個に応ずる学習指導のあり方を追究しようとするものである。 2　研究主題の解決策 （1）　前提条件 ［1］ 個の実態を把握するために，下記の資料を「学習指導カ一ド」にまとめ，活用する。 ・学力診断テスト　・前提条件テスト　・事前テスト ・1学期の成績　　・Y−G性格検査 ・徴候観察記録 ・数学の学習についてのアンケート ［2］ 学習における，個のつまずきや到達度に応じられるような学習コースを準備し，生徒一人一人に確かな学習が成立するように配慮する（分枝型学習）。 （2）　解決策 □1 学習のめあて表によって，単元における学習の流れと，毎時間の学習のめあてをとらえさせる。 □2 形成的評価問題をもとに，自己のつまずきの原因や到達の度合いをとらえ，それに応じた学習コースを選択させ，その学習を進める中で，個に応じた働きかけをする。 □3 自己評価票をもとに，学習についての自已確かめや反省をさせ，その結果に基づき教師がコメントを記入することなどによって，個に応じた働きかけをする。 3　研究主題と抽出生徒とのかかわり A男：おとなしく，ふだんはあまり目立たない方であるが，数学を得意教科としており，積極的に挙手，発表する。等式の性質を使った式変形，移項の考えはよく理解されているが，ax＝b からx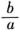＝ の変形にやや不安があるようなので，復習の段階で指名発表させ，より確実なものになるように援助する（上位）。 B子：授業への取り組み方は消極的で，教師の発問に対してもあまり反応を示さない。つまずきやわからない箇所をそのままにしていることが多い。自己評価票を通しての働きかけを強めていきたい。前時の移項について十分理解されていないようであるので，その点から，個別指導にあたる（中位）。 C男：基本的な内容についての理解が劣っている。数学はどちらかといえばきらいのようである。最近，学習全般にわたって自信を失い，あきらめている面が多く見られる。前時までの学習では，移項について符号のまちがいもなくスムーズにすすめている。ただ，文字式の計算でのミスが目立つ。机間指導の中では，この点から働きかけたい（下位）。 （他の5名については省略）

1　単元名　　　　方程式

2　単元の目標

	（1）	方程式は，相等についての条件を式に表したものであり，方程式の解は，その条件を満たす値であることを理解させる。
	（2）	等式の性質について理解させ，それを用いて簡単な方程式の解き方を，筋道立てて考えることができるようにする。
	（3）	等式の性質や移項の考えを用いて，いろいろな形の方程式を解くことができるようにする。
	（4）	方程式を用いて，具体的な問題を解決することができるようにする。

3　指導計画（総時数12時間）
（1）方程式………………………………………………1
（2）方程式の解法……………………………………10
　［1］等式の性質 …………………………………（1）
　［2］等式の性質と方程式の解き方　……………（1）
　［3］1次方程式の解き方…………………………（6）
　　（i）移項の意昧と移項の考えによる方程式の解き方 …［1］
　　（ii）ax＋b=cx＋dの形の方程式の解き方　…［1］（本時）
　　（iii）かっこのある方程式の解き方　…………［1］
　　（iv）係数に小数をふくむ方程式の解き方　…［1］
　　（v）係数に分数がある方程式の解き方 ……［1］
　　（vi）方程式の解き方におけるまとめ　………［1］
　［4］1次方程式の応用……………………………（2）
（3）問題練習……………………………………………1

4　本時の目標

等式の性質や移項の考えを用いて，ax＋b=cx＋dの形をした方程式を解くことができるようにする。

	○1	ax＋b=cx＋dの形の方程式を解くには，bとcxにあたる項を，それぞれ右辺，左辺に移項すればよいことを指摘できる。
	○2	解法手順に従って，ax＋b=cx＋dの形の方程式を解くことができる。

5　準備
　○学習のめあて表
　○学習プリントNo．3
　○自己評価票
　○OHP

6　生徒の実態
　　　　（省　略）