研究紀要第51号 「学習指導の個別化 個に応ずる研究」 -028/080page

前提条件テスト問題

問題			正答率
1	（1）	（−2）＋（＋5）	90
	（2）	3−5	90
	（3）	−4−2	67
	（4）	−5＋7	86
	（5）	3−8＋2	74
	（6）	−4＋7−9	86
	（7）	（−4）×6	100
	（8）	（−28）÷（−4）	76
	（9）	12÷（−3）	81
2	（1）	2÷□＝	100
	（2）	□÷10＝	95
3	（1）	6m−m	38
	（2）	8y＋13y	98
	（3）	−7x＋6 x	69
	（4）	3 x−7x＋x	50
	（5）	−3x＋4＋4 x−5	36
	（6）	−4（5 x−4）	31
	（7）	×12	29
	（8）	−6×	17
4	（1）	（P14参照）	57
	（2）		88
	（3）		57
	（4）		79
	（5）		19
	（6）		55
平均			67

前提条件テストの問題1と問題3は，「1次方程式が解ける」ためには，完全に習得しておかなければならない既習事項である。しかし，これらの問題については満足のいく結果ではなかった。

問題1は，正負についての基本的な四則計算であるが，正答率が90％に達したのは（1），（2），（7）の3問で，残りの6問はそれに達しなかった。特に，（1），（2），（3），（4）のうち3問誤答した下位群の5名については個別に指導した。この5名についてのテストの得点（正答率）は次のようになっている。

生徒	前提条件テスト	事後テスト
S　No．3	11点（44％）	5点（33％）
S　No．4	6点（24％）	7点（47％）
S　No．9	12点（48％）	12点（80％）
S　No．22	14点（56％）	12点（80％）
S　No．26	6点（24％）	2点（13％）

これによると，S No．9とS No，22はよく回復し，事後テストでは正答率80％であった。他の3人は，事後テストの得点が低く，前提条件を回復することができなかったと考えられる。

問題3は，文字式の基本的な計算8題からなっているが，正答率が70％に達したのは問（2）だけで，問（1），（5），（6），（7），（8）はいずれも40％を割っている。これらについては，方程式を解く学習の中で，めあて表や学習プリントの働きかけによりつまずきを解消し定着させるよう努めた。

次に，前提条件が定着しているか否かが，事後テストにどのようになって現れるかを，個々の問題について検討した。前提条件テストと事後テストの問題の中から，関連の深い問題を2題一組にし，その正誤を次のような表にした。ここでは，三組の例を示すことにする。

表5−1

＼ 前提条件テスト 事後テスト ＼		3−（4）		計
		○	×
3−（6）	○	19	14	33
	×	2	7	9
計		21	21	42

表5−1の問題
　3−（4）　3x−7x＋x
　3−（6）　3 x＋8＝5 x−7

表5−2

＼ 前提条件テスト 事後テスト ＼		3−（6）		計
		○	×
3−（7）	○	13	22	35
	×	0	7	7
計		13	29	42

表5−2の問題
　3−（6）　−4（5x−4）
　3−（7）　3x＋5（x−4）＝2

表5−3

＼ 前提条件テスト 事後テスト ＼		3−（8）		計
		○	×
3−（10）	○	6	7	13
	×	1	28	29
計		7	35	42

表5−3の問題
　3−（8）−6×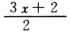
　3−（10）　 − ＝1

表5は，事後テストと前提条件テストとの正誤の関係を示しており，○は正答，×は誤答を表している。また，表5−1中の数値19は3−（4）（前提条件テスト）と3−（6）（事後テスト）の両方に正解した人数であり，数値14は，前提条件テストで×，事後テストで○の生徒数を示している。表5−2，表5−3についても同様である。

これらの表より，前提条件に相当する問題を正答した生徒は，事後テストで対応する方程式を正しく解いていることがわかる。また，前提条件テストで×でも，事後テストで○の生徒がかなりいるが，この生徒は，方程式を解く学習の中で，学