研究紀要第54号 「教育課程の実施に関する研究」 -037/071page

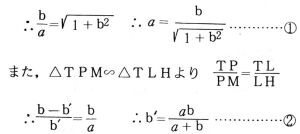
したがって,内接する正ｎ角形,正２ｎ角形の周の長さをそれぞれ２Ａ,２Ａ’とし,外接する正ｎ角形,正２ｎ角形の周の長さをそれぞれ２Ｂ,２Ｂ’とすれば

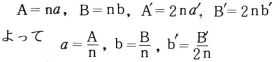
これらを１（マル囲み１）,２（マル囲み２）に代入すると

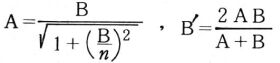
ゆえに,単位円に内接および外接する正２ ⁿ⁺¹ 角形( ｎ＝1,2,3,・・・) の周の長さをそれぞれ２Ａｎ　２Ｂｎとすると,次の漸化式が成り立つ。

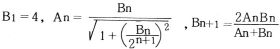
この漸化式により,Ａｎ　Ｂｎ　(ｎ＝1,2,3,・・・)は,下の図のように次々と求められる。

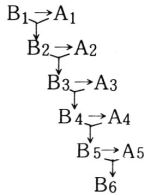
流れ図は図４のようになる

　　　　　図　４

[ 計算の結果と考察 ]
　表４は,半径１の円に内接および外接する正２ ^N+1 角形の周の長さの２分の１の値を表しており,パソコンで作成した。

表４　円周率の計算

　表４からわかるように,Ｎ＝１５すなわち正 65536 角形のとき, ＝Ｌｎ＝ 3.1415926 となっており,これによって,円周率の値は小数点以下７けためまでは 3.1415926 であることがわかったことになる。なお, π のけた数を多く出そうとする場合には Machin の公式などを使えば求めることができる。ここでのねらいは円周率の発見にある。

(4) 区分求積法 (定積分)

区間(ａ,b)をｎ等分し,図５のようにｎ個の長方形の面積をそれぞれI ₁ ，I ₂ ，I ₃ ・・・Inとし

　＝　Ｓｎとすると
Ｓｎ＝Ｓｎ−１　(ｎ≧１),ただしＳｏ＝０

　　　　　 図　５

例４　放物線　ｙ＝Ｘ 2 と直線　Ｘ＝１，Ｘ＝５とＸ軸によって囲まれる部分の面積を区分求積法で求める。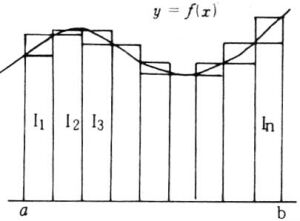

[ ねらい ]
　定積分の学習のなかで,面積を区分求積法で求めることによって,面積の意味と定積分の計算のすばらしさを理解させたい。