研究紀要第117号 「学力向上のための授業改善に関する調査・実践研修 第3年次」 -038/117page

３ まとめ

(1) 単元終了後の調査結果より

1. 「複合図形の面積」

上記の問題は，平成９年度本県通過率３２％・全国通過率４４％であるが，本学級は７６％の通過率であった。ほとんどの児童は，縦１４cm，横２０cmの長方形にした倍積変形による解き方であった。これは，対象の図形を拡張するという考え方が身に付いているものと思われる。これらのことから，「ないものをあるものとして」「別の形にかえて」など授業で学んだ図形感覚あるいは数学的な考え方が身に付きつつあると考えられる。

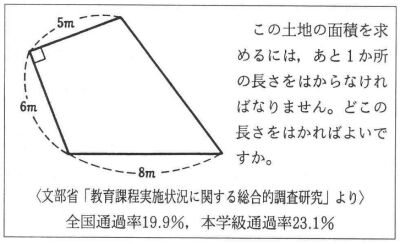
また，下図の問題では，全国通過率よりやや高いが，これは，何が分かれぱ面積が求められるか，必要な長さを自分で探して求めるような活動を授業で取り人れてきたからだと思われる。

2. 「単位量あたりの数量」

この問題では，本県通過率２１％・全国通過率２６％に対して，本学級通過率は４２％であった。問題の「１l(ﾘｯﾄﾙ)あたり」の「〜あたり」について，言葉の意味，考え方の理解が深まったと考えられる。

(2) 児童の変容

1. 下の図形の面積をどのようにして求めるかについて事前・事後において調査したところ，次のような結果が出た。

（上図の問題は東京書籍「新しい算数４年下」より）

※数字は，それぞれの考え方を用いた児童の割合（複数回答可）

このように，事前に比べ，事後では明らかに多様な考え方で面積を求めようという力がついている。

さらに，今回学習した台形の図を使い面積を求めるやり方をした児童が２７％おり，図形のとらえ方が広がってきているとともに，既習の内容を生かそうとする意識がみられる。

2. 【資料４】の「こんでいる」のとらえ方について事前調査では，わずかに２９％の児童が「同じ」ととらえていたが，授業後では５０％に増えている。比べる基準を同じにするというとらえ方が身に付きつつある。

(3) 今後の取り組み

今回の取り組みは，「いかにして数学的な考え方を身に付けるか」についての実践であった。「数学的な考え方」は単元の限られた時間内だけでは，身に付けることができるものではなく，今後，関連した領域でどのような指導ができるか，年間を通しての実践に取り組んでいきたい。

研究協力校・協力員	福島市立清明小学校
	遠藤直樹 教諭