福島県教育センター所報ふくしま　No.18（S49/1974.11） -003/025page

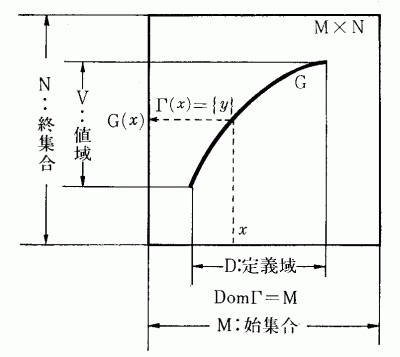
例を示そう。
〔例1〕集合M{=a,b,c,d}、集合N={1,2,3}
対応fが次のように定義されるものとする。

f：

a→f(a)=2 b→f(b)=3 c→f(c)=2 d→f(d)=3

このとき、ｆは関数である。ｆの図表示は次のようである。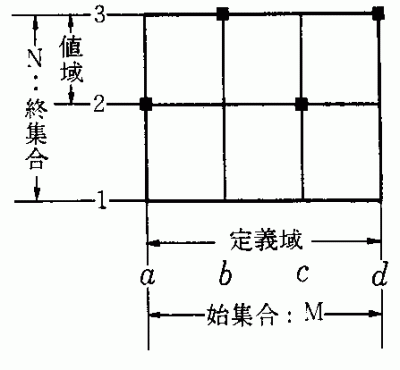

※定義域と始集合Mは等しい。また定義域Dの任意のxに対しΓ(x)がNのただ1つのの要素から成っていることがわかる。

ところで、関数の定義を学習させるなら、当然、対応の定義も学習させなければならないだろう。

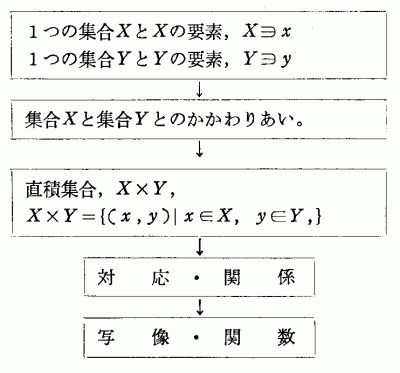
このような順序によれば関数の槻念をまとめあげていくのにつごうがよいように思われる。そこで、対応についての定義にふれてみたい。

対応の定義を、岩波書店：現代数学概説 I、に求めると「直積 M×Nの任意の部分集合をGとする。Gの要素、(x,y)のMへの射影xの集合をP _γM GまたはP _γ1 GまたはDで表わす。Gの要素(x,y)のNへの射影yの集合を、P _γN GまたはP _γ2 GまたはVで表わす。もちろん、D⊂M、V⊂N、xを集合Mの要素とするとき、(x,y)∈Gとなるようなyの集合を、G(x)で表わし、M⊃Aであるとき(x,y)∋Gなるx∈Aが存在するようなyの集合を、G(A)で表わす。G{x}≠φとなるのは、x∈Dとなるときに限り、また、G(x)、G(A)はいつでも⊂Vである。
(G,M,N)なる組が与えられたとき、MからNヘの一つの対応が与えられたといい、対応を一つの文字、たとえばΓで表わすのである。Mを対応Γの始集合、NをΓの終集合、GをΓのgraphという。また上のDをこの定義域(domain)、VをΓの値域(image、range：ensemble des Valeurs)といい、P=DomΓ、V=ImΓと書き表わす。」
と記述されている。
二つの集合M、Nの直積M×Nについては、「M×NはMの元aとNの元bとのなす順序づけられた対(a,b)の集合である。M×Nの二つの元(a,b)、(a',b')はa=a'、b=b'のときに限って同じものとするのである。・・・」
と定義している。対応を定義によって図示すれば次のようになる。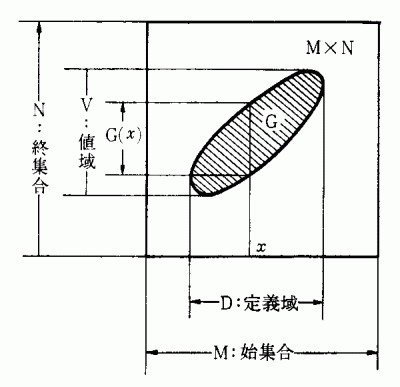

例を示そう。

[例２]	集合M={a,b,c,d} 集合N={1,2,3,}

対応fが次のように定義されてるものとする。

f：	a→f(a)={2} b→f(b)={2,3} c→f(c)={2,3}