福島県教育センター所報ふくしま　No.18（S49/1974.11） -004/025page

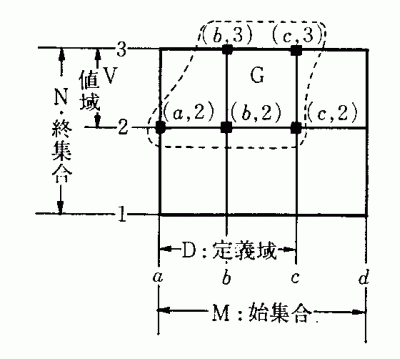
G = {(x, y)} | x∈D, y∈V, y∈Γ(x)}
明らかに
G ⊂ D × V ⊂ M × N
である。

M×N={ ( a, 1) ( a, 2) (a, 3) ( b, 1) ( b, 2) ( b, 3) ( c, 1) ( c, 2) ( c, 3) ( d, 1) ( d, 2) ( d, 3) }
G = { ( a, 2) ( b, 2) ( b, 3) ( c, 2) ( c, 3) }

始集合 M = { a, b, c, d }	定義域 D = { a, b, c }
終集合 N = { 1, 2, 3 }	値域 V = { 2, 3 }

この図からも、始集合 M ≠ 定義 Dであり、始集合 Mの要素が一価ではないことがわかる。
対応Γを図式を用いて表すことによって、より明確なものとすることも必要であろう。
〔例2〕を図式化すれば、次の通りである。

※ 対応の例

〔例1〕は次のように図式化される。

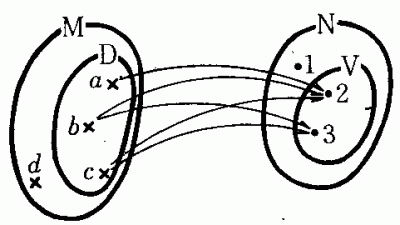
※ 関数の例

次に直積集合について、例を示そう。

[例3]	M = { a, b, c, d } N = {1, 2, 3 }

の二つの集合が与えられている。Mの1つの要素xとNの1つの要素yをとる。このとき順序対(x,y)をすべて書きならべれば、

( a, 1) ( a, 2) ( a, 3) ( b, 1) ( b, 2) ( b, 3) ( c, 1) ( c, 2) ( c, 3) ( d, 1) ( d, 2) ( d, 3)

この順序対すべての集合は直積集合である。

M×N={ (x, y)|x∈M,y∈N}である。

これを図示すれば次のようになる。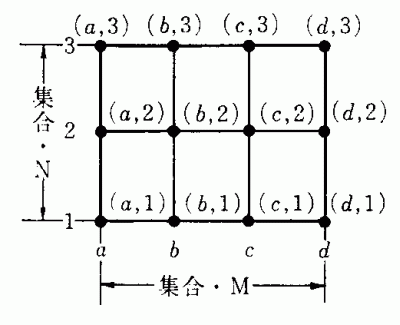

関数の定義に到達するまでに、始集合と定義域との関係、終集合と値域との関係、始集合と終集合との直積、そして対応、という順序をたどることは、関数の概念をまとめあげていくのにつごうがよいだろう。ということで述べてきたのであるが、数学的に厳密である定義は、必ずしも概念をわかりやすく説明したのものでないので実際の指導にあたっては、その概念から得られる具体的なイメージとはかけはなれることが多いようである。
しかし具体的なイメージや印象からかけはなれることが多いからといって、定義に厳密性や抽象性、論理性を失ってしまえば、なんにもならなくなる。
関数の定義は、その激しい史的変遷にとらわれることなく、むしろ現代数学の概念を志向しながら、小学校、中学校、高等学校の児童生徒の発達段階と認識にそっておこなわれることが重要であろう。
よく関数的思考の育成とか、関数的見方、考え方の指導とかいわれているが、これは、集合と集合、集合と要素などの相互関係を、関連して考えることを意味しているのではないかと思う。簡単に表現するなら、関数的思考つまり、functional thinkingとは、「関係において考える。」ことなのであろう。この「関係において考える」ということは、「二つの集合における対応の関係を考える。」ということのように思えるのである。このことは人間の思考の作用とか、機能から考えてもうなづけるように思われるが、あまりにも自分につごうのよい解釈であると、おしかりを受けるかもしれない。