福島県教育センター所報ふくしま　No.27（S51/1976.8） -008/026page

図-1　中心差を求めるための誇張したモデル

図-2　道差を求めるための透明球によるモデル

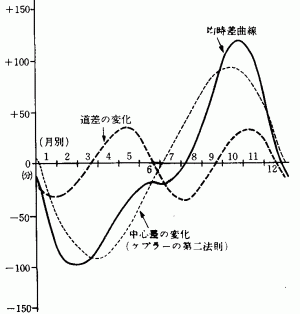
図-3　中心差，および道差のグラフから均時差を求める過程を示すグラフ

aはa'(共通),　bはb',　cはc',　dはd'のように)。

　（5）　赤道と黄道にあらかじめはりつけておいた糸をはずして,それぞれを春分点を共通にしてしらべる。

　(6）　その結果,図-2のb'とb",c'とc"・・・・・・のように，黄道と赤道との間には差がみとめられる。

　（7）　この角度差を,時間(分「ふん」単位)になおして,グラフに記入する(この角度差は長さの差として求められるが,aからdまでは,90 ^。 であるので,これを案分すれば角度が求められる)。

　以上の様な順で実習を進め,図-3の道差の変化グラフを作る(図中の破線)。

　4.　グラフによる均時差の作図

　前述の2,　および3の実習の結果として,図-3の中心差の変化,道差の変化のグラフが得られる。

　この二つのグラフを合成する(コンパスなどをもちいて合成された点を求めれば,簡単にできる)。

　その結果,図の実線のグラフが得られる。もちろん,このグラフのたて軸の目盛は,前述のとおり，モデルが誇張されているので上下の振幅が大きく出ている。

　5.　おわりに

　均時差の指導は,単に中心差,道差を説明的に述べ,終わらせる場合が多いが,　2,　3で述べたような,ねらいをはずさずに実習を通じて,実感として学習させるような心がけが必要である。

　そして，その実習活動の中で，科学的な物の見方，考え方が身につき,科学の方法が体得されていくものと思う。

　地学は,白然を学習の基盤としているだけに,自然から直接データを集め,それをもとに学習を発展させていくことができるという恵まれた教科である。

　一方,学習領域は広まり,深みを増して,生徒達の周囲の自然のみにとどまらず,いわゆるグローバルな物の見方も重視されて来ている。

　そのためには,世界各地のデータや,宇宙空間における多くのデータをもとにした,いわゆるドライ・ラボ的な学習形態も多く要求されてきている。

　現在,地学の学習の手法として前述の二つのタイプが考えられるが,その学習内容に適応した学習形態を選択し進めるべきである。いずれにしても, 探究の過程の重視 は全体を通じ含み得るものであることをつけ加えたい。