福島県教育センター所報ふくしま　No.35（S53/1978.2） -007/026page

いことは，すぐに証明されますが，マチンはこの公式を どのようにして発見したのか。実は，私もこの問題に興 味を持ちましていろいろ調べてみましたが，これについ て書いてある本は見当りませんでした。それで，自分な りに，以下のように考えてみました。

　θが小のとき が成り立つ。 

　いま，4倍すると　π/4≒0.785　となる角Aを考えま すと

　A≒0．196

そこで，0．196に近い単位分数を考えますと，これは 1/5です。そこで， 　となる角αを考えますと,1/5は小ですから,αはほぼ1/5に近い値をとり, 4αはπ/4に近い値となりあす。したがって,　 　は 　に近い値となります。 実さい，加法定理によって，

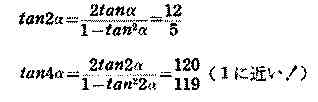
すなわち，4αはπ/4よりもごくわずかだけ大きな値です。

そこで，この差をβとして

とおき，このβの値を，加法定理を用いて次のようにし て求めます。

これらを 1）に代入して

このようにしてマチンの公式が，導き出されました。

　同じように，1倍，2倍，3倍すると，それぞれとπ/4と なる角を考え，さらに，それに近い単位分数を考えるこ とによって，

などの公式も導き出せました。

　次に，マチンの公式から，ラザフォード，ステルマー ，ガウスの公式を導くことを考えてみました。これらの 公式は，すべて単位分数で表されています。それで 

　この式から，ｑ，ｐの整数解が得られるプログラムを組 んで電卓に計算させますと，分解式イ（丸囲み）をみたすｑ，ｐの 値があれば求まります。たとえば　 　は次のよう な（ｑ，ｐ）の値によって分解可能であることがわかりま した。

• （70，−99），（213，−1958），（226，−4155） （237，−28322），（238，−56883），（240，57361） （241，28800），（252，4633），（265，2436） （408，577）・・・

　

これらをマチン公式に代入して，ステルマーの公式が得られました。この公式から，ガウスの公式はすぐ導かれます。

問い 　最後に，なぜπの値を，そんなに何桁も計算す るのですか。

答え 　実用的には，πの値は小数点以下せいぜい10桁 もあれば十分でしょう。それを，コンピューターで，何 桁も計算する理由は，次の2つです。

　ひとつは，πの値がどんなものであるか，どんな数字 の連なりであるかを知りたいという知的好奇心から，も うひとつは，コンピューターの調整やテストのため，さ らにはその性能を知るためです。