福島県教育センター所報ふくしま　No.41（S54/1979.6） -010/038page

―正規分布表は,どのようにして作るのですか―

教科教育部　渡　辺　十　三

　話は少し古くなりますが,国公立大共通一次試験 54年1月13，14の両日に渡って実施され，その結 果の得点分布，平均点（636.1点），標準偏差（134.3 点）などが，大学入試センターから，2月6日の新 聞紙上に発表されました。そして，ある新聞では， 今回の試験の得点分布が，およそ正規分布をしてい るので，自分の得点から，自分が全体の中で，およ そ上から何％の位置にあるかを，正規分布表を用い て知る方法についても簡単にのべてありました。

　ふつう，正規分布表といわれているものは，平均 値が0，標準偏差が1の正規分布（これを標準正規分布といいます）曲線

　　　　　　　　　　　　

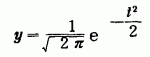
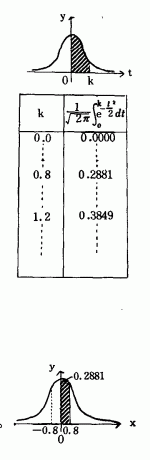
において，右図kの値と， それに対応する斜線部分の 面積（確率）とを表にした ものをいいます。右の表は その一部です。ここで，点 は，平均から，標準偏差の k倍ずれていることを示す 値です。また，この曲線と x軸とで囲まれた部分の面 積は1で，y軸は，この面 積を2等分していますので y軸の左右の部分はそれぞ れ0.5となります。それで， たとえば，平均から，標準 偏差の0.8倍ずれているも のは，全体の中で，上から 0.5−0.2881＝0.2119 すなわち，約21％の位置に あることがわかるわけです。 また，この曲線は，y軸に 関して対称ですから，平均 から，標準偏差の−0.8倍ずれているものは，全体の 中で，上から0.5＋0.2881＝0.7881，すなわち，約 79％の位置にあることがわかります。

　たとえば，今回の共通一次試験で，798点の人は， 自分の得点が，平均点から標準偏差の

　（798−636.1）÷134.3≒1.2

倍ずれていますから，この表によって，全体の中で 上から，0.5−0.3849＝0.1151，約11〜12％の位置 にいることがわかる，というわけです。

　この正規分布表は，統計の本はもちろん，高校の 教2A，数3，応用数学の教科書のうしろに，付表 としてかかげられてあり，極めて大切な表なのです が，どうしたわけか，この表のつくり方について， くわしく書いてある本はありません。それで，よく いろいろな方々から，正規分布表は，どのようにし て作るのですか，という標題のような質問をされま す。そこで，今回は，私の作った正規分布表につい て，その作成法をのペることにします。

　さて，正規分布は，平均値mと，標準偏差бによ って決まる分布なので，この曲線はいろいろあるわ けですが，実は，ちょっとした変数変換をすること によって，結局図のように，標準正規分布の場合に 帰結されることがわかっています。にの部分の説明

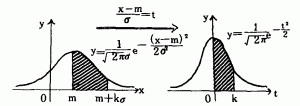
は，教3の教科書にくわしく書いてあります。）

このようなわけで，

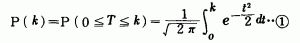
　として，このkの値と，それに対する確率

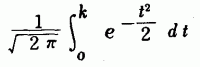
を表にしたものが，正規分布表なのです。つまり， 正規分布表の実体は，この定積分であったわけです。