福島県教育センター所報ふくしま　No.41（S54/1979.6） -011/038page

ですから，kにいろいろな値を与えて，それに対す るこの定積分の値を求めて表にすればよい，という ことになります。ところが，実はこの定積分の計算 は，なかなか一筋なわではいかないのです。正攻法 で攻め切ることができないのです。そこで，ちょっ と思考の方向転換を行ってみます。正攻法で攻め切 れないときは，搦手からとよくいわれます。そこか ら，この定積分を，以下のように攻め切ることがで きました。

　関数e ^x は，

のように無限級数に展開されます。この式のxに、

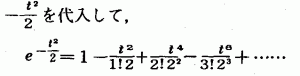
したがって，1（丸囲み数字）

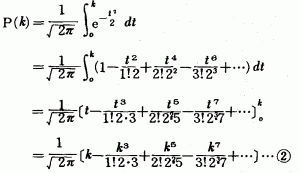
となりますから，この右辺の値を計算すればそれで よいわけです。たとえば，k＝1のとき

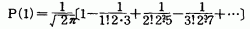
となり，この右辺の値を求めればよいのです。だが， ちょっと待って下さい。この式の右辺は，実は無限 に続いているのです。一体どれだけの項数を計算す れば，どれだけ正しい値が求まるのか，はっきりし ないので困ってしまいます。

　2（丸囲み数字）の〔　〕の中の無限級数は，正の項と負の項と が互い違いにでてくる級数で，このような級数を交 項級数といいますが，交項級数においては，一般に 次のことが成り立ち，実は，上の問題はきれいに解 決されます。関数f（x）が，次のように，条件Aを みたす交項級数に展開されているものとします。

f（x）＝U ₁ −U ₂ ＋…＋（−1） ⁿ⁻¹ U _n ＋（−1） ⁿ U _n＋1 ＋…

（ただし、条件A：U _n ＞U _n＋1 ， n ＝1，2，…をみたす）

このとき，f（x）≒U ₁ −U ₂ ＋…＋（−1） ⁿ⁻¹ U _n

としますと，項打ち切りによる誤差Eは，

E＝（−1） ⁿ ｛U _n＋1 −U _n＋2 ＋U _n＋3 −……｝

＝（−1） ⁿ {U _n＋1 −（U _n＋2 −U _n＋3 −（　）……）}

ここで，条件A：U _n ＞U _n＋1 ， n ＝1，2，…より，この｛　｝の中の（　）の値はすべて正になりますから，

｛U _n＋1 −（U _n＋2 −U _n＋3 −…｝＜U _n＋1

　∴　|E|＜U _n＋1 ………………3（丸囲み数字）

これは，項打ち切りによる誤差の大きさは，その次 の項の大きさを越えないということを示しています。 したがって，あらかじめ，小数点以下何桁まで正し い値が必要であるかを決めておけば，3（丸囲み数字）の関係から 第何項までこの級数を計算すればよいかがわかるわ けです。交項級数2（丸囲み数字）は，はたして条件Aをみたして いるでしょうか。もし，みたしていれば，項打ち切 りによる誤差の評価が，3（丸囲み数字）によってなされうまくゆ きます。2（丸囲み数字）においてUn−U _n+1 との差は，

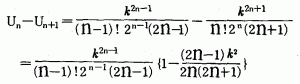
と変形でき，結局，U _n −U _n＋1 の正，負は，｛　｝の値の正，負 によって決まります。｛　｝の中のうしろ

と変形され，kは高々5ぐらいまでの値についてわ かればよいのですから， n を大にすると4（丸囲み数字）は1より 小にできます。よって，このとき{　}＞0，従っ て，Un＞U _n＋1 となって，ある大なる自然数N以上 で2（丸囲み数字）は，条件Aをみたすことがわかります。簡単の ため，k＝1，2，3，4　と整数のときについて 調べてみますと，（※）点＝1，2のときは， n ≧1で 条件Aをみたし，k＝3のときは， n ≧4で，k＝ 4のときは， n ≧7で条件Aをみたしていることが わかりますから，2（丸囲み数字）の級数の，これらの範囲の項ま での和をとれば，項打ち切りによる誤差の評価がで きます。

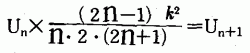
を用いて，次々に項を求めるプログラムを作り，項 打ち切りによる誤差の大きさが，指定した値よりも 小になるまで加えるようにしました。