福島県教育センター所報ふくしま　No.102（H04/1992.3） -014/038page

　ここでは,数学科の例を通して,中学校の教科に対する情意面の測定用紙の作り方を中心にしながら,共通的な評価方法の在り方を考えることにした。
情意面の測定用紙を作成する手順
　情意面のみならず,測定用紙を作成するときは,一般的に次のような手順を踏む場合が多い。

＜測定用紙作成の手順＞

［はじめ］
｜
＜観点の決定＞	・測定したいものをイメージできる表現 （例）「学習への関心」、「授業の準備」 「教科の印象」、「数学の生かし方」
｜
＜項目の収集＞	・観点ごとに20個程度 ・特定場面を詳細に記述したもの
｜
＜文章表現の工夫＞	・測定対象の生徒が理解できる表現 （中学生用なら小学5〜6年生程度の表現）
｜
＜予備調査の実施＞	・収集回答数は項目数の4〜6倍程度
｜
＜信頼性＞	・月2回の測定で、回答の一致度が高いか
｜
＜妥当性＞	・測定したいものを確かに測定しているか
｜
＜使いやすいか＞	・実際に使用するときに問題はないか （例）短時間で実施できるか,本音に迫っているか
｜
＜解釈しやすいか＞	・結果の解釈が一様であるか ・生徒理解に貢献するか
｜
［完成］

測定用紙作成の具体的な方法
　以下の報告は,上記の作成手順に従って進めた一例である。
1.　観点の決定から予備調査結果処理まで
ア　観点の決定
　ブルーム理論によると,「情意面の深い部分よりも浅い部分に共鳴している生徒は多く存在する」ということになる。そこで各レベルの観点をおおむね次のように設定し,項目を収集した(具体的項目は略す)。
<受け入れ> 算数科で培った数や図形に関する直観的好印象
<反応> 計算することや問題を解くことの楽しみ
<価値づけ> 数学科の授業や学習への積極的な取り組み
<組織化> 習慣化された学習態度や問題解決意欲
イ　予備調査の結果
　各レベルごとに4項目を選定し,昭和61年12月に,F県の中学3年生151名を対象に実施した。回答は5件法(はい,まあまあ,どちらでもない,あまり,いいえ)で求めた。各レベルの総得点は20点である。
回答を分析した結果,図1のようになった。このグラフから次のことを読み取ることができる。

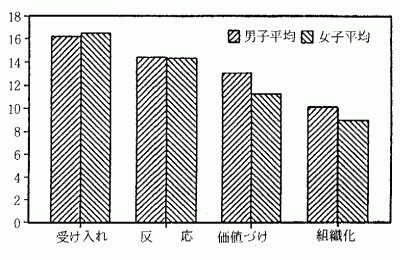
図1　各レベルの平均

・レベルが深化していくにつれて,回答の