福島県教育センター所報ふくしま　No.113（H07/1995.2） -014/038page

取り上げて「柱体」の単元に入ったりするのである。

このような教材は，単元全体の見通しをもたないとうまくいかないが，生徒とともに数学を追究していくという観点からみると，有効な教材なのである。

ところで，中学校２年の三角形の学習で，次のような課題を提示すると，生徒は疑問や当惑を感じながらも関心を示し，意欲的な取り組みをするようになる。

次の三角形の面積を求めなさい。

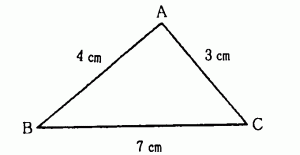
この図からは三角形の高さがわからない。高さを求めるために作図をする生徒も出てくるだろう。すると，「おかしいな，三角形がかけない」と気づくだろう。「面積がない？」このようにして，「三角形ＡＢＣをかくためには，三角形の間にどんな関係がなければならないのだろうか」という学習課題を自ら設定するに至るのである。

(2) 数学的なよさや有用性があること

中学校２年で扱う式の計算の導入課題として次のような問題がある。

地球を大きな球と考えたとき，赤道のまわりに地球から１ｍ離してひもを張ったとすると，その長さは赤道のまわりよりどれほど長くなるだろうか。

最初に生徒に数値計算をさせて大変だと実感させれば，文字を使って式をつくることのよさが分かり，文字を使うことの有用性や便利さに気づくだろう。このように導入の段階で数学的なよさや有用性に気づかせる教材を配することは重要なことである。

ところで，教材の選択を小・中・高校一貫の流れで考えたとき，関数的なものの見方・考え方を具体的な場面で実感させることは，大切なことである。これらの例として，次のようなオープンエンドな教材が考えられる。

Ａ君は遊園地に遊びに行った。観覧車に乗りたいと思って並んでいる。このとき，関数関係としてどんなものが考えられるだろうか。

これらの教材では，生徒を最終的にどこに着地させたいかの目的を明確に定めておくことが必要である。

(3) 発展性があること

生徒に「今度もやってみるぞ」というような欲求をもたせるためには，発展性のある教材の提示が必要である。発展教材は導入教材や学習課題と類似したものが望ましく，いたずらに難しい教材である必要はない。例えぱ，(1)で述べた1(マル1)の教科書の問題を学習した後，2(マル2)の高校入試問題に取り組めば，恰好の発展教材となるのである。

３．おわリに

教材研究で留意しなければならないことは，生徒の実態に即した教材の選定である。

新しい学力観に立った教材研究では，生徒が主役であり，教師との二人三脚で数学を追究していくことが大切であろう。