福島県教育センター所報ふくしま「窓」　No.138（H15/2003.2）-009/036page

「総合的・発展的な学力試験」問題例
出題項目　平方根の発展、文章読解

下の文章を読んで、後の問題に答えなさい。
〈平方根（2乗根）の復習〉
　　2乗して7となる数のうち、正の数をと書くことを勉強しました。 　 　 　　　はどのくらいの大きさの数でしょうか。
　　だから、を小数を使って表すと、＝2……となります。すなわちの整数の部分の数値は2です。
〈3乗根、4乗根、5乗根、………〉
　同じように、3を3回かけ算すると27だから、a³＝27を満たすaの値は3です。このことを27の3乗根は3であると言います。
　次に5乗根について考えてみたいと思います。

100の5乗根はいくらでしょうか。すなわちa5＝100を満たすaの値はいくらでしょうか。星の明るさ（星の等級）を使って、考えてみましょう。

〈星の明るさ（星の等級）〉
　星空を眺めていると様々な輝きの星々が見えます。ギリシャ時代には、全天の中で肉眼で見える最も明るい約20個の星を1等星、最も暗い星を6等星としました。その後、1等星が6等星の100倍の明るさの星であることが発見され、星の明るさを等級で表すことにしました。

　　（ゆかりと太一郎の会話）
　　　〜星空を眺めながらゆかりと太一郎が会話をしています。〜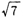

ゆかり	「きれいな星ねえ。」
太一郎	「ほんとだね。ギリシャ時代から人は星を見るのが好きだったんだよ。当時の人はあそこに見えるベガのように最も明るい星を1等星と決めて、順々に2等星、3等星と、……6等星まで等級をつけたんだ。」
ゆかり	「へえ。ということは1等星は6等星よりも6倍明るいということなの?」
太一郎	「いや、そうは単純じゃないんだ。1830年頃に、ハ-シェルという人が1等星の明るさは6等星100個分の明るさである事をやっと発見したんだよ。」
ゆかり	「ということは6等星の100倍の明るさが1等星ということね。」
太一郎	「そういうこと。」
ゆかり	「じゃあ、1等星は2等星の何倍の明るさになるの?」
太一郎	「1等星は2等星のa倍の明るさ、2等星は3等星のa倍の明るさ、………として、下のように考えるんだ。
	つまり、1等星が6等星の100倍の明るさであるから という式が成り立つんだよ。」
ゆかり	「具体的に、aはいくつなの?」
太一郎	「それはねえ。例えぱaを2と考えると 　　　a×a×a×a×a=2×2×2×2×2=32
	aを3と考えると 　　　3×3×3×3×3=243
	だから、aの値は、2と3の間と考えられるわけだ。さらにaを2.5と考えると 　　　2.5×2.5×2.5×2.5×2.5=97.65625
	aを2.6と考えると 　　　2.6×2.6×2.6×2.6×2.6＝118.81376
	だから、1等星は2等星の約2.5倍の明るさということになるね。」
ゆかり	「ということは5等星は6等星の約倍の明るさ、4等星は6等星の約倍の明るさということね。」
太一郎	「その通り。じゃあ、もしも"一1等星"という星があとすれば、どのくらいの明るさの星であるか。説明してごらん。」

　

問題

1	9の平方根（2乗根）を求めなさい。
2	8の3乗根を求めなさい。
3	上の文童中の問い「100の5乗根はいくらでしょうか。」の答えはおよそいくらであるか、文章を読んで分かる値を小数第1位までの値で答えなさい。
4	を小数で表したとき、整数の部分の数値を求めなさい。
5	50の3乗根を小数に直したとき、整数の部分の数値を求めなさい。
6	にあてはまる最も簡単な式を、、に適当な数字を入れなさい。ただし、�A、�B、は小数第1位までの数値で答えなさい。
7	最後の太ー郎の問いに対して、ゆかりに代わってあなたが答えなさい。