7　2次関数のグラフと最大・最小,方程式・不等式(数1「2次関数」)
関連:前　座標と式(中1),1次関数(中2),2次方程式(中3)後　いろいろな関数(数2)

1　つまずきの内容
(1）2次関数のグラフを利用して,最大値・最小値を求めることができない。
(例)y＝x2-2x-2(-1≦x≦2)における最大値・最小値を求めよ。
与式を,y＝(x-1)2-3と変形して,頂点(1,-3)を求めてグラフをかくことはできても,グラフを見て,最大値・最小値がどこなのかがわからない。

(2)2次不等式を2次関数のグラフを利用して解くことができない。
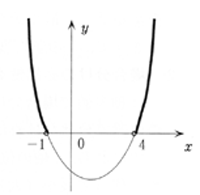
(例)x2-3x-4＞0を満たすxの値の範囲を求めよ。
与式を,(x+1)(x-4)＞0と変形し,右のようにグラフをかくことはできるが,グラフのどの部分がy＞0となっているのかが解らない。また,それに対応したxの範囲を不等式で表すことができない。


2　つまずきの分析
(1)xの値の変化に伴ってyの値が変化することをグラフから読みとれない。
中学2年の「1次関数の変域」の学習から,xの変域に対するyの変域は,xの範囲の両端のyの値を考えればよいという印象が強く,グラフのyの値の変化が見えない。高校入試における,y＝ax2の形の関数の最大・最小に関する問題の正答率も低い。
(「4　高校入試についてのつまずきの分析」で後述)

(2)条件を満たす点の集合という「領域」的な考え方がわからないために,「グラフを用いて不等式の解を求めること」がどういうことかわかっていない。
中学校では,y＞0となる座標平面上の点の集まりという考え方はしていない。領域については,高校でも,数学に続いて履修する数学の「図形と方程式」で初めて学習する考え方であるために,直観的に理解できない生徒はつまずく。
2次不等式の場合,「グラフのy＞0の部分に対応するxの値の範囲」ということが,x軸との位置関係からだけでは理解できないために,不等式の解が把握できない。その結果,パターン化・公式化して「数学は暗記」にしてしまい,グラフを使わないと解きにくい「解はすべての数」や「解なし」の場合はできないということになる。