4　2次関数の最大・最小や2次不等式にグラフを利用する指導例
(1)2次関数の最大・最小

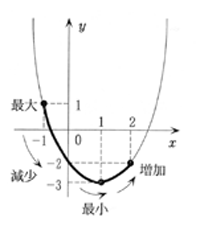
(例)y＝x2-2x-2(-1≦x≦2)における最大値・最小値を求めよ。

y＝(x-1)2-3……頂点(1,-3)
グラフ上で,x=-1からx＝2まで点を動かして,yの値の変化を示すと関数の増減がわかりやすい。
xの値が,-1から2まで変化するのにしたがって,
1）出発点のyの値は,1
2）yはそこから減少を続け,頂点でyの値が最小
3）yはその後増加して,終点のyの値が,-2
ここで,グラフの値の変化を見て,最大値・最小値がわかる。(最大値は1）と3）を比較させる)
(注)数直線や座標軸になぜ矢印がついているのかについて,確認するとよい。
中学校では,矢印を付けていない。(中・高ともに教師はこの違いをあまり認識していない)

(2)2次方程式・2次不等式

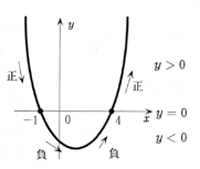
(例)2次関数y＝x2-3x-4において,x軸との交点を求めよ。
また,2次不等式x2-3x-4＞0を満たすxの値の範囲を求めよ。

y＝(x+1)(x-4)として,yの符号を考える。
1）x＜-1⇒x2-3x-4＞0(y＞0)
2）x＝-1⇒x2-3x-4＝0(y＝0)
3）-1＜x＜4⇒x2-3x-4＜0(y＜0)
4）x＝4⇒x2-3x-4＝0(y＝0)
5）4＜x⇒x2-3x-4＞0(y＞0)
のように,グラフのyの値の変化に注目させる。

(工夫1)グラフの矢印に沿って点を動かして,x座標とy座標がどう変化するかを,動かす点の座標をx軸,y軸に値を対応させながら示す。
(工夫2)y＞0,y＝0,y＜0の部分を色分けしてわかりやすくする。
(工夫3)工夫1,工夫2をコンピュータグラフィックスを利用して示す。